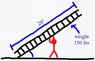
The amount of force you need to raise the ladder depends on how fast you want it to move, but for simplicity's sake we can assume you exert enough force to balance gravity. An infinitesimally small increase in force above this will raise the ladder, so you can consider this to be the minimum force required. Also important is how far away from the fulcrum the force is. These two quantities are combined in the calculation of moments.
Starting with gravity, recall that it always acts directly downwards, but to calculate moments, you will need to use trigonometry to calculate the component of gravity perpendicular to the ladder. Assuming the ladder is uniform along its length, you can assign a centre of mass (think about where that might be). This is the point from which all of the ladder's weight will act, at all times. To get the moment due to gravity, you just multiply the component of force perpendicular to the ladder by the distance along the ladder from the fulcrum to the centre of mass.
Now, to balance this with pushing. You can work out the distance along the ladder at which the person pushes using trigonometry with their feet, their hands and the fulcrum forming a right-angled triangle. This distance may not be the same as the distance at which gravity acts. It is not correct at this point just to make the forces equal; the moments must be equal. So if F is the pushing force and x is the distance of this force from the fulcrum, you will need to divide the moment you calculated earlier by x, and you have your force.
You'll find that x and the component of the gravitation force perpendicular to the ladder both depend on the angle, thereby introducing it into your final equation.
I've tried to give you mostly conceptual help to allow you to come up with the equations yourself, but if any step is unclear just leave a reply :)