Forward euler calculations for position and orientation

[sabatier]

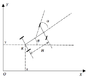
Hi, I'm trying to compute the equations of motion for a car as shown
in the attached image.

α = steering angle
θ = orientation of the car relative to the world coordinate system

Say you're given the linear velocity v and the steering
angle α. How do you compute the position and angle θ for a
particular time?

Any help appreciated.

 

[Cantab Morgan]

I find the problem difficult because a real car has a differential. Without it, a car wouldn't change directions when you turned the wheel, the front tires would just skid. My off the cuff guess is that the angle of steering doesn't give you enough information, but you might have to know something about how the car's differential worked.

In any case, coordinate systems are under your control so you should make them do your bidding. Consider transforming to a frame where the car is at rest relative to the origin, and \theta is zero. Try solving the problem for a motorcycle first, or even a unicycle.