Four bodies connected through a sheave

[Chemist@]

Homework Statement

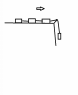
Three bodies with masses m₁ m₂ and m₃ connected with a string through a sheave with a body with mass m₄. The system is moving right. Write the second Newton law for the movement of the objects. Ignore friction.

Homework Equations

2nd law for bodies:
m₄a= m₄g-T(the force of stretching the string)
m₁a= T
m₂a= T
m₃a= T

The Attempt at a Solution

By summing up the last three equation I got:
a(m₁+m₂+m₃)=3T but it is apparently incorrect. The book equation is:
a(m₁+m₂+m₃)=T, how? Where am I wrong at?

 

[BvU]

You want to ask yourself if T is really the same in the various sections.

 

[Chemist@]

Could you elaborate please?

 

[collinsmark]

Could you elaborate please?

I believe what BvU is alluding to is that you are assuming that all sections of the string have the same tension.

Homework Equations

2nd law for bodies:
m₄a= m₄g-T(the force of stretching the string)
m₁a= T
m₂a= T
m₃a= T

While that is often true for a massless string when ignoring friction, it doesn't apply here because the string has masses attached to it. In other words, the tension of the string between bodies m₁ and m₂ is a different value than the tension between bodies m₂ and m₃ and so on.

You can still exploit the idea of tension though, just pick one of the tensions. The books seems to have picked the tension in the string at rightmost side, that passes through the sheave. Don't forget that the three leftmost bodies move together as a group.

 

[BvU]

If the left block feels tension T₁ and is accelerated with acceleration T₁/m₁, the next block feels tension T₁ working to the left. If that block is also accelerated with acceleration a, the net force on block 2 must be m₂a. So it feels a Tension T₂ to the right for which m₂a = T₂-T₁.

et cetera

 

[Chemist@]

I see. When they all add up I get T₃. Thank you very much.