Gopal Mailpalli
- 28
- 2
Self Study
1. Homework Statement
Consider a periodic function f (x), with periodicity 2π,
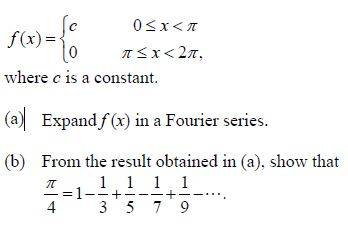
##A_{0} = \frac{2}{L}\int_{X_{o}}^{X_{o}+L}f(x)dx##
##A_{n} = \frac{2}{L}\int_{X_{o}}^{X_{o}+L}f(x)cos\frac{2\pi rx}{L}dx##
##B_{n} = \frac{2}{L}\int_{X_{o}}^{X_{o}+L}f(x)sin\frac{2\pi rx}{L}dx##
##A_{0} = C##
##A_{n} = 0##
##B_{n} = \frac{-C}{\pi r}cos\pi r##
http://imgur.com/a/4Q2oL
1. Homework Statement
Consider a periodic function f (x), with periodicity 2π,
Homework Equations
##A_{0} = \frac{2}{L}\int_{X_{o}}^{X_{o}+L}f(x)dx##
##A_{n} = \frac{2}{L}\int_{X_{o}}^{X_{o}+L}f(x)cos\frac{2\pi rx}{L}dx##
##B_{n} = \frac{2}{L}\int_{X_{o}}^{X_{o}+L}f(x)sin\frac{2\pi rx}{L}dx##
The Attempt at a Solution
##A_{0} = C##
##A_{n} = 0##
##B_{n} = \frac{-C}{\pi r}cos\pi r##
http://imgur.com/a/4Q2oL