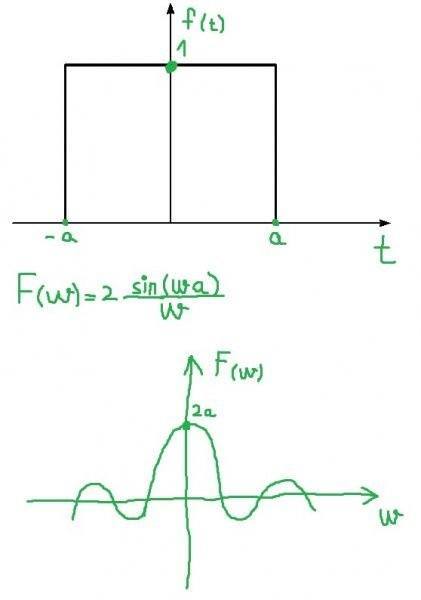
The discussion centers on the importance of the Fourier transform, particularly in contrast to Fourier series. While Fourier series represent periodic signals using discrete frequencies, the Fourier transform allows for the analysis of non-periodic signals by utilizing continuous frequencies. This transformation is crucial in various applications, including digital signal processing, where it simplifies complex calculations by converting convolutions in the time domain into multiplications in the frequency domain. Additionally, the Fourier transform aids in analyzing electrical circuits by converting time-domain signals to the frequency domain for easier manipulation and response analysis. Overall, the Fourier transform is essential for working with a wide range of signal types in engineering and mathematics.