- #1
Bauxiet
- 18
- 1
Hi everyone,
I am an electromechanical engineering student. The last few days I am trapping into some confusion about some things. I am just going to state my question underneath.
Question:
First question:
As they learned me at the university. When you draw a free body diagram it doesn't mind in which direction you draw a force. In the end, you get the same magnitude but with a different sign, what means that the force will be pointing in the opposite direction. This is correct?
For example the exercise below. What if a drew the N-force in the opposite direction? Would it give me the same numeric solution but with a different sign? For my experience, the angular acceleration that i had to calculate was a different numeric solution when I had drew the N-force in the opposite direction.
For example I had to calculate the angular acceleration. I drew the N-force counter the y-axis. So the equation would be: -N - 20*g = 0 <=> N = -20*g ! This means I have drawn my force in the wrong direction. Do I have to change the value to N= 200 N or do I have to calculate with the N = -200 N until the end when the exercise is done? (and use the - 200N in momentum equations for example).
My second question:
Must a (acceleration) and alfa (angular acceleration) always go in the same direction? For example: My a is pointing to the right (positive) direction. Can my alfa turn counter clockwise or must it turn clockwise (and does it care which direction positive is? or must i choose clockwise positive because the right direction for a is positive?)
I hope my questions are a little bit clear. I am experiencing some problems with this topic. I just have to know if the directions of forces/angular accelerations are important or it will all give the same result if you just follow the convention until the end of the exercise. Or do i have to change the value during the exercise. (for example (do i have to change N = -200 N to N = 200 N during the exercise and fill in the positive number in the other equations?)
Thank you very much in advance.
Greetings,
Bauxiet
When having a dynamic or static problem. Take for example a dynamic problem. Like underneath:
The exercise is written in dutch, sorry for this.
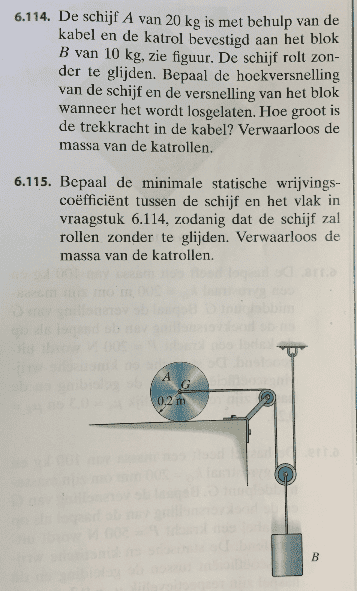
This is my solution:
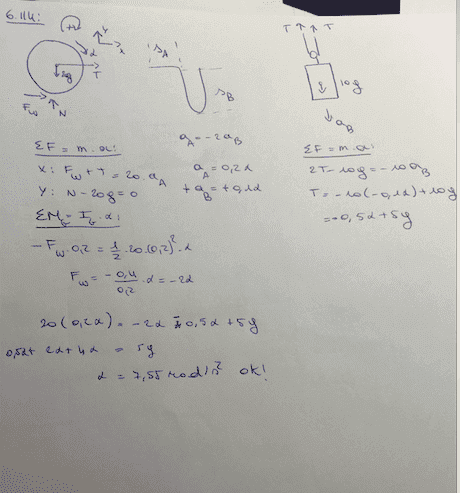
I am an electromechanical engineering student. The last few days I am trapping into some confusion about some things. I am just going to state my question underneath.
Question:
First question:
As they learned me at the university. When you draw a free body diagram it doesn't mind in which direction you draw a force. In the end, you get the same magnitude but with a different sign, what means that the force will be pointing in the opposite direction. This is correct?
For example the exercise below. What if a drew the N-force in the opposite direction? Would it give me the same numeric solution but with a different sign? For my experience, the angular acceleration that i had to calculate was a different numeric solution when I had drew the N-force in the opposite direction.
For example I had to calculate the angular acceleration. I drew the N-force counter the y-axis. So the equation would be: -N - 20*g = 0 <=> N = -20*g ! This means I have drawn my force in the wrong direction. Do I have to change the value to N= 200 N or do I have to calculate with the N = -200 N until the end when the exercise is done? (and use the - 200N in momentum equations for example).
My second question:
Must a (acceleration) and alfa (angular acceleration) always go in the same direction? For example: My a is pointing to the right (positive) direction. Can my alfa turn counter clockwise or must it turn clockwise (and does it care which direction positive is? or must i choose clockwise positive because the right direction for a is positive?)
I hope my questions are a little bit clear. I am experiencing some problems with this topic. I just have to know if the directions of forces/angular accelerations are important or it will all give the same result if you just follow the convention until the end of the exercise. Or do i have to change the value during the exercise. (for example (do i have to change N = -200 N to N = 200 N during the exercise and fill in the positive number in the other equations?)
Thank you very much in advance.
Greetings,
Bauxiet
When having a dynamic or static problem. Take for example a dynamic problem. Like underneath:
The exercise is written in dutch, sorry for this.
This is my solution:
 (welkom dus)
(welkom dus)