Free body diagram and force vectors

[samjohnny]

Homework Statement

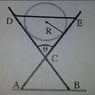
Attached, where AC=BC=2R and CD=CE=3R. I need to work out the force the cylinder exerts on the cross section (in order to work out the moment at C). So first I'm trying to work out the free body diagrams for this system. Is it as I've attached? How do I draw the tension vector? And then I'm having a hard time defining and decomposing the force vectors in terms of theta, mg etc. Can anyone lend a hand?

 

[tiny-tim]

hi samjohnny!

we need to know a little more …

are CD and CE hinged at C?​

So first I'm trying to work out the free body diagrams for this system. Is it as I've attached? How do I draw the tension vector?

it would be easier to start with the free body diagram of the cylinder

your puzzlement as to how to draw the tension is caused by choosing the wrong body

a free body diagram shows all the external forces on a body, so it won't show up on a body for which it's an internal force!

you need to do it for one rod

(the symmetry makes that a lot easier than it would otherwise be)

 

[samjohnny]

hi samjohnny!

we need to know a little more …

are CD and CE hinged at C?​

it would be easier to start with the free body diagram of the cylinder

your puzzlement as to how to draw the tension is caused by choosing the wrong body

a free body diagram shows all the external forces on a body, so it won't show up on a body for which it's an internal force!

you need to do it for one rod

(the symmetry makes that a lot easier than it would otherwise be)

Hey! Thanks for the reply.

Yeah they're connected at C. Cool, I see what you mean. I'll take another crack at it.