burhan619
- 7
- 0
I have a question for two scenarios (see the diagram attached):
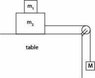
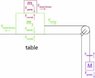
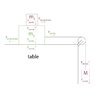
1) When the two blocks on the table are at rest, the static friction the table exerts on the bottom block is counteracting the tension in the rope, resulting in a net force of zero. Is there any static force being exerted by the bottom block on the top block? I don't think there should be any, since there is no horizontal force acting on the top block.
2) Suppose M was massive enough to start descending, overcoming the static friction threshold of the bottom block. Also suppose that the top block starts to slip away from the bottom block. Which way does the kinetic force the bottom block exerts on the top block point? And what's exerting the horizontal force it's counteracting?
Thanks in advance.
1) When the two blocks on the table are at rest, the static friction the table exerts on the bottom block is counteracting the tension in the rope, resulting in a net force of zero. Is there any static force being exerted by the bottom block on the top block? I don't think there should be any, since there is no horizontal force acting on the top block.
2) Suppose M was massive enough to start descending, overcoming the static friction threshold of the bottom block. Also suppose that the top block starts to slip away from the bottom block. Which way does the kinetic force the bottom block exerts on the top block point? And what's exerting the horizontal force it's counteracting?
Thanks in advance.