- #1
franceboy
- 51
- 0
Hi there, i have some problems with the following homework. It would be nice, if you help me :)
A well isolated house is located in a region where the sun does not shine and the temperature is constantly about 5°C outside. The house is empty except a full fridge with the constant temperature of -18°C. After a while the house has stabile temperature of 6.5°C. The fridge shall work like an ideal Carnot cooling-machine.
If you turn off the fridge and put it outside, it warms up. After 15 minutes it has a temperature of -12.4 °C and after 30 minutes -8.1°C. The heat capacity of the fridge is C= 80 J/K.
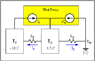
a) Determine the stabile temperature of house if you would have two fridge like in the text above.
b) Calculate the elictrical power in both cases.
c) Determine the maximal temperature of the house, if you would use a bigger fridge with same temperature, kind of working and isolation.
Okay, my idea was that the fridge is heated by the room like it is heated ouside (proportional to the difference of temperature PH->F= k*(TH-TF). Since the fridge`s temperature keeps equal it is cooled all the time, while heating the room.
However, now i was confused: the text says that the house is well-isolated (I thought this means no energy transfer) but then the temperature would increase without stopping because the fridge heats more than it cool (second law). This means the house must be cooled by the outer world like it is heated by the fridge. Is that right?
Homework Statement
A well isolated house is located in a region where the sun does not shine and the temperature is constantly about 5°C outside. The house is empty except a full fridge with the constant temperature of -18°C. After a while the house has stabile temperature of 6.5°C. The fridge shall work like an ideal Carnot cooling-machine.
If you turn off the fridge and put it outside, it warms up. After 15 minutes it has a temperature of -12.4 °C and after 30 minutes -8.1°C. The heat capacity of the fridge is C= 80 J/K.
a) Determine the stabile temperature of house if you would have two fridge like in the text above.
b) Calculate the elictrical power in both cases.
c) Determine the maximal temperature of the house, if you would use a bigger fridge with same temperature, kind of working and isolation.
Homework Equations
The Attempt at a Solution
Okay, my idea was that the fridge is heated by the room like it is heated ouside (proportional to the difference of temperature PH->F= k*(TH-TF). Since the fridge`s temperature keeps equal it is cooled all the time, while heating the room.
However, now i was confused: the text says that the house is well-isolated (I thought this means no energy transfer) but then the temperature would increase without stopping because the fridge heats more than it cool (second law). This means the house must be cooled by the outer world like it is heated by the fridge. Is that right?