reggie
- 4
- 0
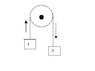
Two blocks are connect by a lght string which passes over a light pulley as shown in the figure. They are released from rest. Block A distance of 1.2m in 1.6 s
http://img149.exs.cx/img149/3595/pulley5uz.th.jpg
1. what is the gain in the kinetic energy of the two blocks?
2.What is the loss in potenial energy of the two blocks?
3.Explain why the two values in parts (1) and (2) differ.
A is 4 kg
B is 6 kg
http://img149.exs.cx/img149/3595/pulley5uz.th.jpg
1. what is the gain in the kinetic energy of the two blocks?
2.What is the loss in potenial energy of the two blocks?
3.Explain why the two values in parts (1) and (2) differ.
A is 4 kg
B is 6 kg
Attachments
Last edited: