MHB Garden Materials Calculator: Calculate Area & More

[lward100]

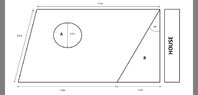
I have tried this a couple of times but no successBefore you buy materials, you need to work out how much you will need. As such, you need to calculate the following:

the circumference of the pond -A
the perimeter of the garden
the patio area -b
the lawn area (minus pond area)
the pond area- a
Please remember to show your workings and give answers to two decimal places!

needs to show all calculations and solutions including the missing height of trapezium near the houseView attachment 8551

 

[HOI]

Exactly what have you tried and where did you have problems?

the circumference of the pond -A
I presume you know that the circumference of a circle of diameter, d, is $\pi d$. Here the diameter is 2.7m.

the perimeter of the garden
Does the "garden" include the patio? If not, the boundary between the patio and the garden is the hypotenuse of a rig[ht triangle in which an angle is 40 degrees and the "opposite side" has length 2.5 m. sin(40)= 2.5/x. You are given all of the other lengths.

the patio area -b
You are told that the length of the leg opposite the 40 degree angle is 2.5 m. The length of the other leg is given by 2.5/x= tan(40). I presume that you know that the area of a triangle is given by (1/2)base times height.

the lawn area (minus pond area)
What is the distinction between "garden" and "lawn"?

the pond area-
The area of a circle is \pi r^2. If the diameter of the pond is 2.7 m, the radius is 1.35 m.

 

[lward100]

Exactly what have you tried and where did you have problems?

the circumference of the pond -A
I presume you know that the circumference of a circle of diameter, d, is $\pi d$. Here the diameter is 2.7m.

the perimeter of the garden
Does the "garden" include the patio? If not, the boundary between the patio and the garden is the hypotenuse of a rig[ht triangle in which an angle is 40 degrees and the "opposite side" has length 2.5 m. sin(40)= 2.5/x. You are given all of the other lengths.

the patio area -b
You are told that the length of the leg opposite the 40 degree angle is 2.5 m. The length of the other leg is given by 2.5/x= tan(40). I presume that you know that the area of a triangle is given by (1/2)base times height.

the lawn area (minus pond area)
What is the distinction between "garden" and "lawn"?

the pond area-
The area of a circle is \pi r^2. If the diameter of the pond is 2.7 m, the radius is 1.35 m.

hi yes the lawn area is the garden

so what is the equation and answer for area of the lawn

area of patio

and can you confirm the calculation and length for the side near the house?

thanks

 

[Wilmer]

Please remember to show your workings and give answers to two decimal places.

You have to show YOUR workings...not ours...
Are you saying you're unable to calculate (as example) area of a circle diameter = 2.7?

Please show your work so far and where you're stuck...we'll check it...

 

[lward100]

Circumference of the pond = pi*D = 2.7*pi = 8.48m

Perimeter of the garden = 6.2+7.4+(2.5÷tan(40))+2.5+5.5

Area of patio = 0.5(2.5)(2.5÷tan(40))

Perimeter of Garden = 6.2+7.4+(2.5÷tan(40))+2.5+5.5 = 24.58m

Area of patio = 0.5(2.5)(2.5÷tan(40)) = 3.72m^2

Area of lawn = area of garden - area of patio - area of pond = 0.5(5.5+2.5+7.4)(2.5÷tan(40)) - 0.5(2.5)(2.5÷tan(40)) - pi(2.7÷2)^2 = 13.5m^2

Area of pond = pi(2.7÷2)^2 = 5.73m^2





The circumference of the pond is 8.48m and each border takes 2m so 8.48÷2 = 4.24 = 5 border bags required therefore cost of border on pond = 5*5.40 = £27



The perimeter of the garden is 24.58m and each panel takes 1.5m so 24.58÷1.5 = 16.37 = 17 panels required.

The number of panels for fencing and decorative trellis is same so cost for both fencing and trellis = (17*6)+(17*8) =£238

Are of patio is 4.08 and each slab covers and area of (0.6)^2 so 4.08÷(0.6)^2 = 11.33 = 12 slabs required and so the total cost will be 12*9.5 = £114

Area of patio 4.08m^2 and each slab covers (0.6)^2 of area so 4.08÷(0.6)^2 = 11.33 = 12 slabs required which means 2 boxes required and so cost = 2*9.5 = £19

Area of patio 3.72m^2 and each slab covers (0.6)^2 of area so 3.72÷(0.6)^2 = 11.33 = 10.34 slabs required which means 2 boxes required and so cost = 2*9.5 = £19

Area of lawn = 13.5 and each bottle of lawn food is covering 3m^2 of area so 13.5÷3 = 4.5 = 5 bottles of lawn food required and hence the cost is 5*3 =£15

Total cost £299

 

[Wilmer]

Perimeter of Garden = 6.2+7.4+(2.5÷tan(40))+2.5+5.5 = 24.58m

Correct...good job!
I'm too lazy to check the rest...