fishingspree2
- 138
- 0
We know that for an infinite sheet of charge, E = λ / 2ε, where λ is the surface charge density. This can be easily found using gauss law and a cylinder perpendicular to the sheet as a gaussian surface. We will end up with something like Qinc/ε = 2E ∫dS, from which we find E = λ / 2ε.
Now say that I want to find the charge for a semi-infinite sheet of charge. A sheet that is infinite in only 1 dimension. If i try to apply Gauss's Law the same way as in the previous case, I end up with exactly the same procedure and answer, which is not correct.
But I fail to see what is different in the application of Gauss Law, between the 1st and the second case.
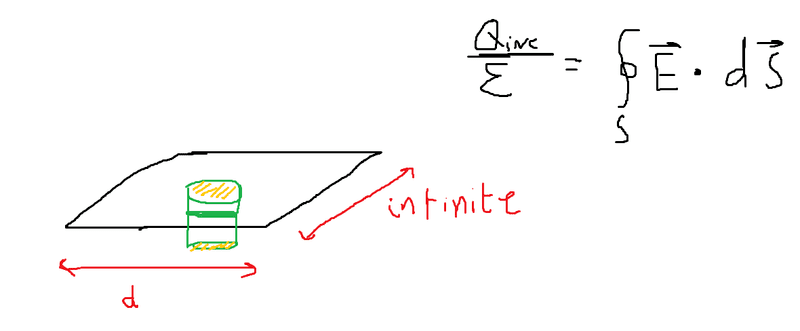
Now say that I want to find the charge for a semi-infinite sheet of charge. A sheet that is infinite in only 1 dimension. If i try to apply Gauss's Law the same way as in the previous case, I end up with exactly the same procedure and answer, which is not correct.
But I fail to see what is different in the application of Gauss Law, between the 1st and the second case.