- #1
Saladsamurai
- 3,020
- 7
! AHH Gauss' Law!
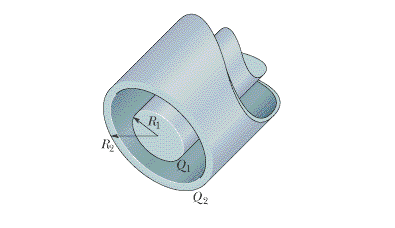
Figure 23-27 is a section of a conducting rod of radius R1 = 1.30 mm and length L = 11.00 m inside a thick-walled coaxial conducting cylindrical shell of radius R2 = 10.0R1 and the (same) length L. The net charge on the rod is Q1 = +3.40 × 10^-12 C; that on the shell is Q2 = −2.00Q1.
a) What is the magnitude and (b) direction (radially inward or outward) of the electric field at a radial distance r=2R2?
What are (c) E and (d) direction at r=5R1?
What is the charge on the (e) interior and (f) exterior surface of the shell?
I'm going to be honest, I slept through most of this class this week (it's like being in @!#$ing morgue!) so I am having some trouble here. ANY help is greatly appreciated
I am sure I need some form of Gauss' Law (since that is the name of the chapter).
I am just not sure which form? can someone help me out here?
I know that [itex]\phi=\frac{q_{enc}}{\epsilon_o}[/itex]
There are many formulae, but this one seems promising since I know the q_enc.
I also know that by the definition of a flux
[tex]\epsilon_o\int\vec{E}\cdot d\vec{A}=q_{enc}[/tex]
I am just a little jammed from here. How can I manipulate that integral? Or better still, what can I use instead of the integral so that I can write it as E=...SOMETHING ?
Homework Statement
Figure 23-27 is a section of a conducting rod of radius R1 = 1.30 mm and length L = 11.00 m inside a thick-walled coaxial conducting cylindrical shell of radius R2 = 10.0R1 and the (same) length L. The net charge on the rod is Q1 = +3.40 × 10^-12 C; that on the shell is Q2 = −2.00Q1.
a) What is the magnitude and (b) direction (radially inward or outward) of the electric field at a radial distance r=2R2?
What are (c) E and (d) direction at r=5R1?
What is the charge on the (e) interior and (f) exterior surface of the shell?
Homework Equations
I'm going to be honest, I slept through most of this class this week (it's like being in @!#$ing morgue!) so I am having some trouble here. ANY help is greatly appreciated
I am sure I need some form of Gauss' Law (since that is the name of the chapter).
I am just not sure which form? can someone help me out here?
I know that [itex]\phi=\frac{q_{enc}}{\epsilon_o}[/itex]
There are many formulae, but this one seems promising since I know the q_enc.
I also know that by the definition of a flux
[tex]\epsilon_o\int\vec{E}\cdot d\vec{A}=q_{enc}[/tex]
I am just a little jammed from here. How can I manipulate that integral? Or better still, what can I use instead of the integral so that I can write it as E=...SOMETHING ?