Dilemma
- 15
- 1
Hello,
1. Homework Statement
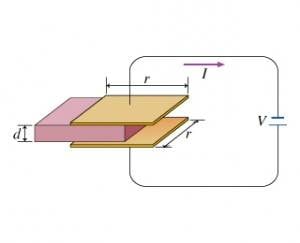
Assuming that the dielectric is inserted at a constant rate, find the current I as the slab is inserted.
Express your answer in terms of any or all of the given variables V, K, r, d, Δt, and ε0, the permittivity of free space.
[/B]
C = ε0 * A / d
[/B]
Q = CV
dQ = dC ⋅ V
I = dQ/Δt
C = ∈ ⋅ A / d = ∈⋅(xr)K / d + ∈⋅(r-x)r / d
dC = ∈⋅(r)K / d - ∈⋅r / d = ∈r(K-1)/d
dQ = dC⋅V
Therefore answer should be ∈r(K-1)V/(dΔt)
However, the correct answer is ∈(r^2)(K-1)V/(dΔt). That means the multiplier "r" is missing. What is wrong with my solution.
Thanks in advance.
1. Homework Statement
Assuming that the dielectric is inserted at a constant rate, find the current I as the slab is inserted.
Express your answer in terms of any or all of the given variables V, K, r, d, Δt, and ε0, the permittivity of free space.
Homework Equations
[/B]
C = ε0 * A / d
The Attempt at a Solution
[/B]
Q = CV
dQ = dC ⋅ V
I = dQ/Δt
C = ∈ ⋅ A / d = ∈⋅(xr)K / d + ∈⋅(r-x)r / d
dC = ∈⋅(r)K / d - ∈⋅r / d = ∈r(K-1)/d
dQ = dC⋅V
Therefore answer should be ∈r(K-1)V/(dΔt)
However, the correct answer is ∈(r^2)(K-1)V/(dΔt). That means the multiplier "r" is missing. What is wrong with my solution.
Thanks in advance.