You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
How Do You Calculate the Length of a Chord and Tangential Line in a Circle?
AI Thread Summary
To calculate the length of a chord and a tangential line in a circle, the radius is essential. The discussion highlights the use of the tangent-chord theorem and the Pythagorean theorem to derive the lengths. The original poster ultimately calculated the chord length as 3.82 using trigonometric functions and geometric relationships. There were also considerations regarding the angles and relationships between various segments of the circle. Clarifications on the definitions and assumptions were necessary to guide the calculations effectively.
Physics news on Phys.org
BvU
Science Advisor
Homework Helper
- 16,212
- 4,925
Oops, the template got lost. Programming error or accidental deletion? Here it is again: :)
2. Homework Equations
3. The Attempt at a Solution [/B]
Also, you want to ask clear questions. "Value of a chord" is not very scientific: Economic value ? Color value ? In this case you want the length.
Seems to me that one needs the circle radius also to make sense of this ?
Homework Statement
2. Homework Equations
3. The Attempt at a Solution [/B]
Also, you want to ask clear questions. "Value of a chord" is not very scientific: Economic value ? Color value ? In this case you want the length.
Seems to me that one needs the circle radius also to make sense of this ?
ChimM
- 17
- 0
Sorry about the template.
Problem statement: [/B]
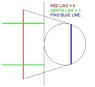
Find the value of the chord (blue line) and at the same time the value of the tangential line.
Given data:
Red line = 6
Green Line = 3
Radius of the Circle = 2
I don't know any equations that can solve the problem :(
I used the area of a trapezoid. But too many unknown.
Homework Statement
Problem statement: [/B]
Find the value of the chord (blue line) and at the same time the value of the tangential line.
Given data:
Red line = 6
Green Line = 3
Radius of the Circle = 2
Homework Equations
I don't know any equations that can solve the problem :(
The Attempt at a Solution
I used the area of a trapezoid. But too many unknown.
BvU
Science Advisor
Homework Helper
- 16,212
- 4,925
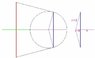
This help ? I see a way to calculate distance top left to center cicle, and then top left to tangent point.
And then there are isomorphic triangles to be found that can help us further...
ChimM
- 17
- 0
BvU said:View attachment 75074
This help ? I see a way to calculate distance top left to center cicle, and then top left to tangent point.
And then there are isomorphic triangles to be found that can help us further...
From there, can I use pythagorean theorem to solve the value of the tangential line? :)
BvU
Science Advisor
Homework Helper
- 16,212
- 4,925
value being length, equation, whatever: yes, I should think so. Didn't work it all out in detail: your job. Finding a possible smarter way is also your job/challenge :)
ChimM
- 17
- 0
Can you give me hints on how can I relate the length of the tangent line to the chord? Pleaseee. Thank you :)BvU said:value being length, equation, whatever: yes, I should think so. Didn't work it all out in detail: your job. Finding a possible smarter way is also your job/challenge :)
BvU
Science Advisor
Homework Helper
- 16,212
- 4,925
Draw AD, calculate |AD|, calculate |AB| .
Look at isomorphic triangles ACE and DCE
then DCE and BCF
Looks like a lot of work. You do some too.
ChimM
- 17
- 0
BvU said:View attachment 75076
Draw AD, calculate |AD|, calculate |AB| .
Look at isomorphic triangles ACE and DCE
then DCE and BCF
Looks like a lot of work. You do some too.
Hmm.. Since, the tangent line and Radius is perpendicular, then it creates a 90degrees. The other side is also 90degrees, would it be right if I use 45degrees for the chord line and the radius? :)
BvU
Science Advisor
Homework Helper
- 16,212
- 4,925
More questions, no work done yet. What about AD and AB?
SSWheels
- 19
- 2
BvU said:Look at isomorphic triangles ACE and DCE
Hmmm ...
It seems that DCE isn't a triangle at all, since the 3 points are collinear!
SSWheels
- 19
- 2
BvU said:View attachment 75074
This help ? I see a way to calculate distance top left to center cicle, and then top left to tangent point.
And then there are isomorphic triangles to be found that can help us further...
There are several assumptions made here:
1) The black lines are all tangent to the circle
2) The vertical tangent line, the red line, and the blue line are all parallel to each other
3) The green lines are perpendicular to the vertical tangent line
4) The red line bisects both green lines
5) The midpoint of the red line is collinear with the center of the circle and the tangent point of the vertical tangent line.
By "value of the tangent line," I assume he means the length of a segment of the vertical tangent line between the points where it intersects the other 2 tangent lines?
Also, the OP doesn't specify which tangent line
BvU
Science Advisor
Homework Helper
- 16,212
- 4,925
Yes, sorry: DCBSSWheels said:Hmmm ...
It seems that DCE isn't a triangle at all, since the 3 points are collinear!
Any results yet from the original poster ?
ChimM
- 17
- 0
BvU said:Yes, sorry: DCB
Any results yet from the original poster ?
I used the tangent-chord theorem to get the length of the chord. Since 2 tangent lines created the chord, it formed a triangle. The chord as the base and the radius as the legs. As shown at the attached picture.
I used sine(45) to get the value of h. Sine 45 × 2 =h
h = 1.41
r - h = 2 - 1.41 = 0.59
Using pythagorean theorem:
2 = sqrt (X^2 + 0.59^2)
X = 1.91 = Half of the chord
2x = whole chord
2 × 1.91 = 3.82
Therefore, length of the chord is 3.82.
Please cite your corrections. Thank you :)
Attachments
BvU
Science Advisor
Homework Helper
- 16,212
- 4,925
The 45 degrees is not correct. I don't understand the reasoning.
"Draw AD, calculate |AD|, calculate |AB| .
Look at isomorphic triangles ACE and DCB "
What did you get for |AD|, |AB| ? Angle EAC ? Angle DCB ? Angle DBF ?
"Draw AD, calculate |AD|, calculate |AB| .
Look at isomorphic triangles ACE and DCB "
What did you get for |AD|, |AB| ? Angle EAC ? Angle DCB ? Angle DBF ?
Similar threads
- Replies
- 9
- Views
- 3K
- Replies
- 7
- Views
- 3K
- Replies
- 11
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 1
- Views
- 1K
- Replies
- 13
- Views
- 6K
- Replies
- 13
- Views
- 10K
- Replies
- 7
- Views
- 10K
- Replies
- 13
- Views
- 4K
Hot Threads
-
Geometry: Similar Shapes
- Started by paulb203
- Replies: 116
- Precalculus Mathematics Homework Help
-
[ASK] Trigonometric Inequality
- Started by Monoxdifly
- Replies: 6
- Precalculus Mathematics Homework Help
-
What does this equation mean?
- Started by inuka00123
- Replies: 12
- Precalculus Mathematics Homework Help
-
Finding polar equation of a shifted cricle
- Started by farfromdaijoubu
- Replies: 6
- Precalculus Mathematics Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 4
- Quantum Physics
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 5
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 10
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math