- #1
Tom Salazar
- 2
- 0
1. Get A from its inverse
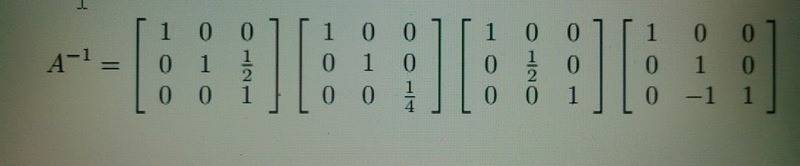3. I believe it has something to do with the theorem that states: E1E2E3...EkA=I
Get matrix A from a series of elementary matrices
- Thread starter Tom Salazar
- Start date
Click For Summary
SUMMARY
The discussion focuses on deriving matrix A from a series of elementary matrices using the identity E1E2E3...EkA=I. It emphasizes the importance of the theorem stating that the inverse of a product of matrices is the product of their inverses in reverse order, represented as (MN)^{-1} = N^{-1}M^{-1}. Participants recommend consulting textbooks for methods to determine the inverse of individual matrices, particularly the method involving the matrix of cofactors.
PREREQUISITES- Understanding of matrix operations and properties
- Familiarity with elementary matrices
- Knowledge of matrix inverses and the cofactor method
- Basic grasp of linear algebra concepts
- Study the derivation of matrix inverses using the cofactor method
- Learn about the properties of elementary matrices
- Explore the application of the theorem (MN)^{-1} = N^{-1}M^{-1} in various contexts
- Practice solving problems involving the composition of elementary matrices
Students and professionals in mathematics, particularly those studying linear algebra, as well as educators seeking to enhance their understanding of matrix theory and its applications.
Similar threads
- · Replies 25 ·
- · Replies 8 ·
- · Replies 2 ·
- · Replies 25 ·