skysunsand
- 38
- 0
Homework Statement
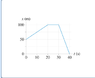
Given the graph in the uploaded screenshot, what is the bicyclist's velocity at t=10s?
Homework Equations
I have been trying to do a slope equation? Rise/run.
The Attempt at a Solution
Tried to do slope equation. Looks like 75/10, which would be 7.5, but that answer is incorrect. Why? It wants to two sig figs, and that is two sig figs...I also have no clue what to do if t= anything else, like 25 or something. Is there a different equation for that? I'm so lost. :(