Debo Industry
- 8
- 0
How did we measure the gravitational constant G = 2.034 x 10 ^ 17 cm ^ 2 and the Earth average density (specific gravity) p = 3.45 g / cm ^ 2 s ^ 2.
PhysicoRaj said:The gravitational constant was measured by Henry Cavendish, using a setup, like this:
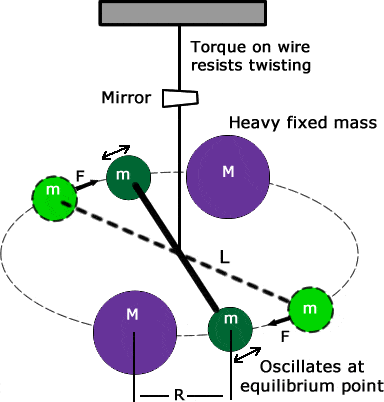
When the lead spheres are moved the gravitational force acting on the other set of spheres induces a force on the wire which twists, and the restoring torque can be equated to the gravitational force as follows:
torque = force * length
τθ=GMm/r2]*l
(where l is the length of bar, τ is the torque per unit angle of twist, θ is the angle of twist caused by the force).
So,
G=τθr2/Mml
θ, angle of twist can be measured by many methods.( in the figure it is measured by laser, and hence u see a mirror).