Gravitational Force: Find Angle for Net F on Particle 1

Click For Summary
SUMMARY

The discussion centers on calculating the angle for the net gravitational force acting on particle 1, which has a mass of 10.0 Kg, due to four other particles each with a mass of 2.5 Kg. The particles are arranged with a distance of 4 cm between them. The possible angles for the net gravitational force to cancel out are provided as options: 30°, 45°, 90°, and 0°. Participants are encouraged to simplify the diagram to facilitate the calculation.

PREREQUISITES
  • Understanding of gravitational force and Newton's law of gravitation
  • Basic knowledge of vector addition and equilibrium
  • Familiarity with trigonometric functions and angles
  • Ability to interpret and simplify physical diagrams
NEXT STEPS
  • Study the principles of gravitational force and its vector components
  • Learn about equilibrium conditions in physics
  • Explore trigonometric identities relevant to angle calculations
  • Practice problems involving multiple particle systems and net forces
USEFUL FOR

Physics students, educators, and anyone interested in gravitational interactions and force calculations in multi-particle systems.

divr
Messages
3
Reaction score
0
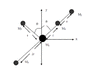
Fig1 shows an arrangement of five particles with masses M1 = 10.0 Kg, M2=M3=M4=M5=2.5 Kg and with r = 4 cm. For what angle (in degrees) of the net gravitational force F on particle 1 due to other particles cancels out.
a)30 b) 45 c) 90 d) 0

(figure is given in the attachment)
 

Attachments

  • phy.GIF
    phy.GIF
    3 KB · Views: 478
Physics news on Phys.org
Well, what do you think? Hint: Can you simplify the diagram at all?
 

Similar threads

Finding the net gravitational force with Vector Notation
  • · Replies 2 ·
Replies
2
Views
2K
Magnitude of net Gravitational Force
  • · Replies 1 ·
Replies
1
Views
5K
Calculating Net Force of 3 Blocks in an Elevator
  • · Replies 9 ·
Replies
9
Views
2K
Why used $\cos\theta$ for $\text{y}$ axis or, gravitational force?
  • · Replies 2 ·
Replies
2
Views
2K
Finding the net gravitational force on a rocket....
  • · Replies 5 ·
Replies
5
Views
2K
Calculating net force on four masses around a center mass?
  • · Replies 4 ·
Replies
4
Views
3K
What is the period of this binary orbit?
  • · Replies 3 ·
Replies
3
Views
2K
Calculating Net Gravitational Force in Equilateral Triangle Configuration
  • · Replies 5 ·
Replies
5
Views
2K
Rate of Gravitational Force (Power)
  • · Replies 5 ·
Replies
5
Views
4K
Determine the direction and acceleration of the bead
  • · Replies 6 ·
Replies
6
Views
4K