Gravitational Force OR Angular Momentum

[mateomy]

My classmates and I are having a debate on how to solve the following problem. We are told that (and this has been posted on this message board before) that a planet of mass M and radius R is moving SLOWLY through a dust cloud of density (rho). Some of the particles will be attracted to the planet. Find the retarding force on the planet from the dust particles.

I think that if you set up a typical gravitational force problem and solve the smaller mass in terms of the mass of the dust you get something as such:

<br /> \frac{-4GM\rho\pi R}{3}<br />

On the other hand a few of the others think that it can be solved using angular momentum….as so:

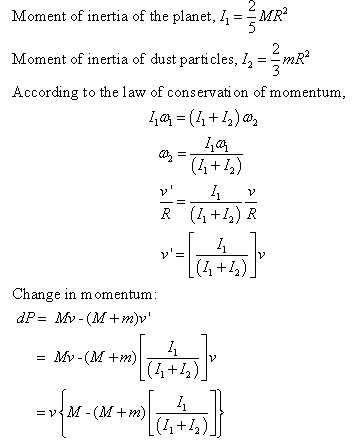
Adding…

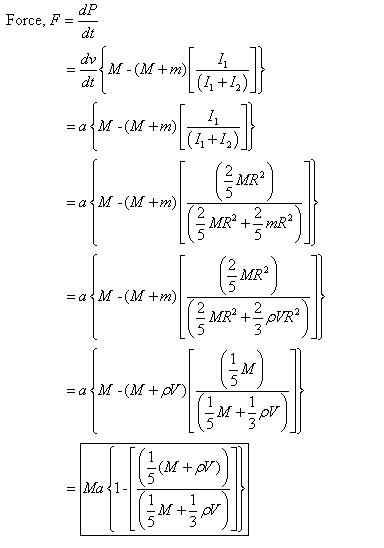
The argument against my idea is that it only treats the planet as if it were going through a cylinder picking up what was only directly in front of it. I don't see that validity in that argument. Can anybody put in a fresh word on the subject? Please?

 

[NascentOxygen]

It's an interesting concept. The planet will pick up all of the dust in its path, plus that which is near enough to it that it can be accelerated into the surface before the forward speed of the planet takes it out of reach. But in addition to this, the entire field of particles will be set into motion, accelerated towards the planet, and all left drifting in its wake (each dust particle left with a component of its velocity in the direction of motion of the planet). The planet will lose momentum as it accelerates even distant dust particles.

I think the maths is beyond me., though I can see it will involve an integration from 0 to infinity.

 

[BruceW]

I guess the most correct way to solve this problem would be to simulate billions of tiny dust particles, and to get the acceleration of each particle, you must calculate the gravitational force due to all other dust particles and the planet, and then there's also the contact force with other dust particles.
This would take a lot of computer power though :)

There's no analytic solution to the problem of gravity between 3 or more objects - its called the 3-body problem (in this case there's a lot more than 3). So to solve, you must find the acceleration on all objects, and numerically calculate what happens for each time step