jozefmak
- 3
- 1
Hi,
I have two similar circuits. One of them is clear for me but I am not sure how the second one works.
Let's start with the clear one:
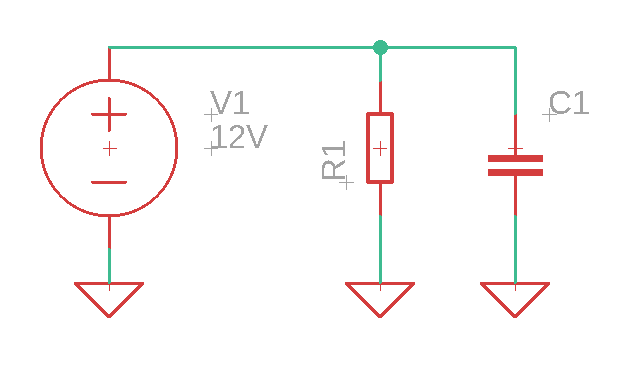
a parallel RC circuit, which is explained here:
At time t = 0s there are zero volts across the resistor because the capacitor is fully uncharged. After some time, the capacitor will get charged to 12V so we will measure 12V across the resistor.
This is the unclear circuit for me:
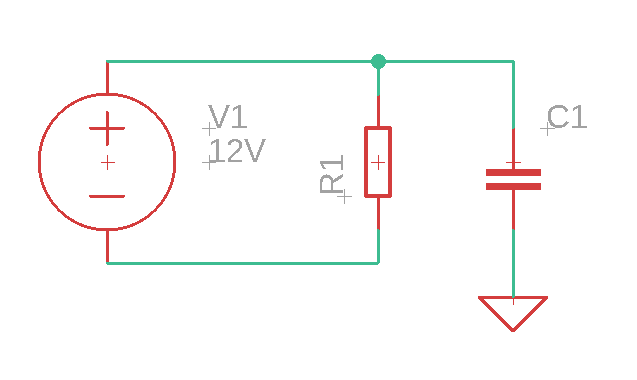
Will the capacitor get charged? (What voltage?)
What voltage are we going to measure at t = 0s across the resistor?
I know that when I remove the capacitor:
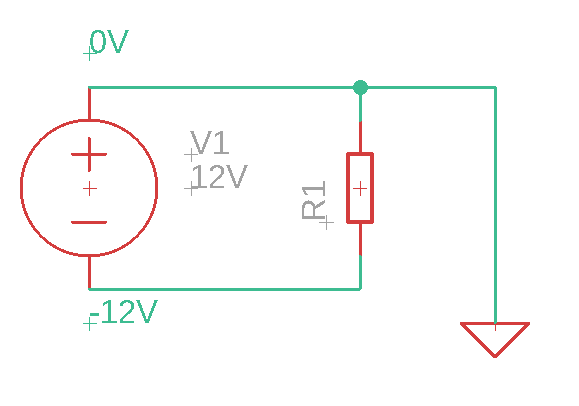
there will be 12V across the resistor at time t = 0s because a positive terminal of battery will have 0V and negative terminal of battery will have -12V (with respect to those 0V). The problem, which makes this circuit unclear for me is the capacitor.
I have two similar circuits. One of them is clear for me but I am not sure how the second one works.
Let's start with the clear one:
a parallel RC circuit, which is explained here:
At time t = 0s there are zero volts across the resistor because the capacitor is fully uncharged. After some time, the capacitor will get charged to 12V so we will measure 12V across the resistor.
This is the unclear circuit for me:
Will the capacitor get charged? (What voltage?)
What voltage are we going to measure at t = 0s across the resistor?
I know that when I remove the capacitor:
there will be 12V across the resistor at time t = 0s because a positive terminal of battery will have 0V and negative terminal of battery will have -12V (with respect to those 0V). The problem, which makes this circuit unclear for me is the capacitor.