myusernameis
- 56
- 0
hahaha uhhhh operations of e
i'm reading this online math help thing, and i can't seem to memorize how/why this is
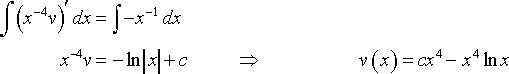
how did they get this?edit* how did they get the answer from the left to the right side of the arrow?
i know this is prob. the beginner stuff, but i forgot this from a long time ago. and don't worry, this is only one step of the equation, not the whole answer.
Thanks!
Homework Statement
i'm reading this online math help thing, and i can't seem to memorize how/why this is
Homework Equations
how did they get this?edit* how did they get the answer from the left to the right side of the arrow?
The Attempt at a Solution
i know this is prob. the beginner stuff, but i forgot this from a long time ago. and don't worry, this is only one step of the equation, not the whole answer.
Thanks!