Hanging Sign Problem: Find Angle & Distance from Ceiling

[KatieLynn]

Homework Statement

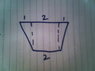
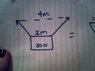
If you are hanging a sign from the ceiling with two wires, each with a safe working load of 20N. The hooks at the top of the sign are 2.0 meters apart while the hooks in the ceiling are 4.0 meters apart. A) If the sign weighs 30N what is the minimum angle to the horizontal the wires can be to safely hang the sign, and B) how far from the ceiling is the top of the sign?

Homework Equations

F=MA
I'm not sure if that it or not... but that's my best guess.

The Attempt at a Solution

I attached the picture(s) I drew to attempt to solve it. I'm not sure what angle to solve for or how to solve for it.

 

[Astronuc]

OK, the tension in one line must be less than 20 N, and each line must bear half the weight (through symmetry). Half the weight is 15 N, if the line was vertical, but since the upper fixtures are 4 m apart and the fixtures on the sign are 2 m apart, then the top of line is offset by 1 m from the bottom of the line, so the line is at an angle.

With the line at an angle, the tension in the line must increase since the vertical component must be 15 N, and the tension must never exceed 20 N. What angle achieves that?

With that angle, what is the length of line for a horizontal displacement of a 1 m (horizontal leg/base) of a right triangle?