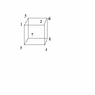
Here's a pretty simple proof of the case for rectangular loops. This is specific to base 10, but it can be easily generalized:
The array of numbers looks like this:
1 2 3 ... d
d+1 d+2 d+3 ... 2d
...
Where there are d numbers in each row. Now the rectangular loop, which has length 2n, looks something like this:
[x] [x+1] [x+2] ... [x+k]
[x+d] x+d+1 x+d+2 ... [x+d+k]
[x+2d] x+2d+1 x+2d+2 ... [x+2d+k]
...
[x+l*d] [x+l*d+1] [x+l*d+2]... [x+l*d+k]
Where the bracketed terms make up the number, with x being the first digit and x+d the last. k and l are the width and height of the rectangle. The (n+1)th digit is x+l*d+k, and the sum of the first and (n+1)th digit is 2x+l*d+k. The sum of the second and (n+2)th is (x+1) + (x+l*d+k-1), which is 2x+l*d+k. It is easy to see that the sum of the ith digit and the (i+n)th digit is always 2x+l*d+k, which from here on I'll call 'm'. Also, from here on I'll call the ith digit di. So d1=x, and di+di+n = 2x+l*d+k = m.
Now the number, which I'll call N, can be put in the form:
N = 10^n x + y
where:
x = d_1 10^{n-1} + d_2 10^{n-2} + ... + d_n
y= d_{n+1} 10^{n-1} + d_{n+2} 10^{n-2} + ... + d_{2n}
We know that 111...11 with n 1's divides 10n-1. So if it divides N, it must also divide:
N -(10^n-1)(x)= 10^n x + y-(10^n-1)x = x + y
which is:
(d_1 10^{n-1} + d_2 10^{n-2} + ... + d_n ) + (d_{n+1} 10^{n-1} + d_{n+2} 10^{n-2} + ... + d_{2n})
= ((d_1+d_{n+1}) 10^{n-1} + (d_2+d_{n+2}) 10^{n-2} + ... +(d_n +d_{2n} )
= m 10^{n-1} + m 10^{n-2} + ... + m
= m (111...11)
which completes the proof.
edit: this also works if the string starts somewhere else in the loop or goes around the otherway. all this changes is which sums are in which decimal places, but since theyre all m anyway, you get the same result.
edit 2: I just thought of a few generalizations. This will work for any shape constructed like so: Make a contour with n squares. Copy it, rotate it by 180 degrees, and put the second piece wherever you want (use it to form a closed shape if you want, but you don't need to). The number is formed by starting at any point on one of the contours and continuing in one direction around it and in the same direction around the rotation until you get back to where you started. This covers the diamond shape.
I admit this is a little confusing. Here's an example: if your shapes are Ls, you could start at the corner of one L, go up the long side, than across the short side of the other one, down its longs side, and finally across the short side of the original one to get back to the start. The second L must be rotated by 180 degrees, but could be anywhere you want it. They could form a rectangle, not touch at all, or overlap, just as long as you go around the right way.
This number will have 2n digits, and is divisible not just by 111...11 with n ones, but also with k ones for any k that divides n.