Having trouble graphing a Volume problem

[BlackMamba]

Hello again,

Once I get this graphed correctly, I don't see any problems as to why I couldn't solve it. But for now I have a question about graphing this volume problem.

The problem says to find the volume generated by rotating the region bounded by $y=e^x$, $x=0$, and $y=\pi$ about the x-axis.

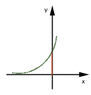
I have a picture of what I my graph would look like. The green curve is the line $y=e^x$, and the rust colored line is, $x=0$. My question is where do I graph $y=\pi$ ? Is it as simple as placing the line at y = 3.14?

Thanks for taking a look. It is greatly appreciated.

 

[BlackMamba]

I still am unsure about this. I could use the help. Thanks.

Actually I think I got it. But if you could look at confirm or deny what I have come up with I would appreciate it.

 

[fire]

I'd love to confirm what you have, however, for some reason the attachment is "pending approval." I can't view it.

Left boundary is a vertical line at x=0. Right and bottom boundary is y=e^x. Top boundary is y=pi. There's an intersection point where y=e^x and y=pi meet. It should look like a triangle. Then you rotate about the x-axis.

I didn't bother attaching a picture since attachments on this forum need some approval.

 

[radou]

...My question is where do I graph $y=\pi$ ? Is it as simple as placing the line at y = 3.14?

Yes, it is as simple as placing a line parallel to the x-axis at y = 3.14.

 

[BlackMamba]

Thanks fire and radou.

Fire ~ Your description is what my graph looks like so thanks again.