RingNebula57
- 56
- 2
Hello everyone. I'm new into thermodynamics and I have a question about the gained and lost heat in any type of process of an ideal gass ( linear, non- linear). In the picture below we have a process suffered by a gas in p-v coordinates. The process is linear ( for simplicity) with P=Po-aV; where a and Po are givee constants. The process goes form 1 to 2. If we want to find the points in which the heat cancels and the temperature reaches its maxima, we have to draw the adiabat and isotherm that are tangent to the linear function. The points where they are tangent corespond to the maximal temperature and heat=0 respectively.
Those points are not that hard to find. Let's call the point in which the adiabat is tangent "a" and the point in which the isotherm intersects "i".
Now, I have been reading from several textbooks that between 1-i the difference in temperature is greater than 0 and from i-2 the diffrence in temperature is less than 0. So far so good. Than it was written that between 1-a the heat is gained and between a-2 the heat is lost . Ok. And than I thought that , if the heat between 1-a is gained and heat= (temperature difference) * (number of moles) * ( molar heat) than it means that (molar heat)>0 between 1-i and <0 between i-a. And between i-2 the molar heat has to be again greater than 0. Now this is the part where I don't understand. How can you actually prove that between 1-i and a-2 the molar heat > 0 and that between i-a molar heat < 0 .
Than I had been thinking about polytropic processes in which it can be proven that for a process of form:
P*V^n=constant, than the molar heat ( cosntant) of the polytrope is C=Cv + R/ (1-n) , where C= molar heat, Cv= molar heat at constant volume, R= ideal gas constant, n= polytrope index.
So let's say that all the points that belong to our linear process are the tangency points of some polytropes ( like the isotherm , adiabat) to the linear function of the process. So to every point on our line coresponds a specific molar heat C = Cv + R/ (1-n) where n in the polytropic index of the polytrope that goes trough that point. Now as we ascend in pressure and we descent in volume ( I'm talking about the points on the linear process) we can imagine that the polytropichyperbolas will be less and less steaper , so we can prove that for n<(adiabatic index) than C<0, and for n>(adiavatic index) than C>0.
Now this doesn't corespond to our solution . From the solution we have that between 1-i C>0 , but I get that C<0.
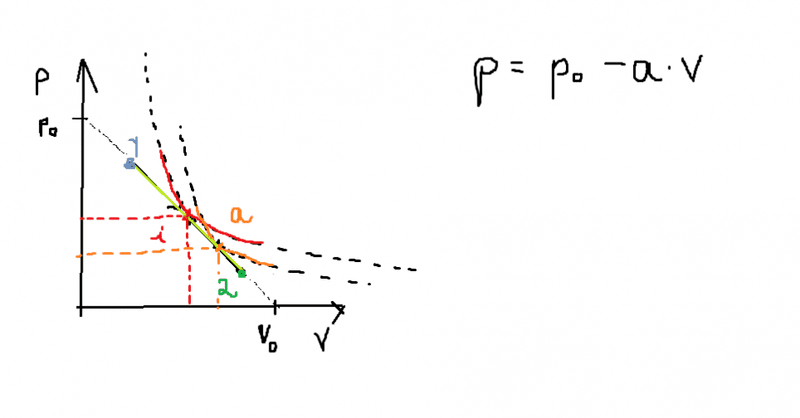
Where is my mistake , this is driving me crazy.
Thank you
Those points are not that hard to find. Let's call the point in which the adiabat is tangent "a" and the point in which the isotherm intersects "i".
Now, I have been reading from several textbooks that between 1-i the difference in temperature is greater than 0 and from i-2 the diffrence in temperature is less than 0. So far so good. Than it was written that between 1-a the heat is gained and between a-2 the heat is lost . Ok. And than I thought that , if the heat between 1-a is gained and heat= (temperature difference) * (number of moles) * ( molar heat) than it means that (molar heat)>0 between 1-i and <0 between i-a. And between i-2 the molar heat has to be again greater than 0. Now this is the part where I don't understand. How can you actually prove that between 1-i and a-2 the molar heat > 0 and that between i-a molar heat < 0 .
Than I had been thinking about polytropic processes in which it can be proven that for a process of form:
P*V^n=constant, than the molar heat ( cosntant) of the polytrope is C=Cv + R/ (1-n) , where C= molar heat, Cv= molar heat at constant volume, R= ideal gas constant, n= polytrope index.
So let's say that all the points that belong to our linear process are the tangency points of some polytropes ( like the isotherm , adiabat) to the linear function of the process. So to every point on our line coresponds a specific molar heat C = Cv + R/ (1-n) where n in the polytropic index of the polytrope that goes trough that point. Now as we ascend in pressure and we descent in volume ( I'm talking about the points on the linear process) we can imagine that the polytropichyperbolas will be less and less steaper , so we can prove that for n<(adiabatic index) than C<0, and for n>(adiavatic index) than C>0.
Now this doesn't corespond to our solution . From the solution we have that between 1-i C>0 , but I get that C<0.
Where is my mistake , this is driving me crazy.
Thank you