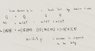Heat problem, determine mass of ice cube?

In summary, the conversation discusses a situation where the answer for the heat absorbed by ice does not match the expected value. It is determined that the mistake may be in using the heat of fusion constant for solid water, which should be used in two separate calculations for the ice and water phases.
  • #1
gibson101
47
0
My answer is 12.9 grams, and the correct answer is supposed to be 11.9 grams. I cannot figure out why? Note. the answer i got is 12.9, and not 11.06. I know for this situation, the heat absorbed by the ice equals the heat lost by the water and aluminum, and since there is a phase change from a solid to liquid then i need the heat of fusion constant for solid water, which in kcal/kg which is 79.7. Now I am thinking that this is where my mistake is, because temperature remains constant during a phase change. Therefore, I cannot put 16-(-8.7)? I have to write it out into two separate m*c*deltaT's?
 

Attachments

  • Screen shot 2011-06-18 at 5.53.02 PM.JPEG
    Screen shot 2011-06-18 at 5.53.02 PM.JPEG
    11.5 KB · Views: 558
  • 11.jpg
    11.jpg
    16.4 KB · Views: 467
Last edited:
Physics news on Phys.org
  • #2
Yes, you need two separate m*c*deltaT-s for the ice, as c of ice is different from that of water it becomes after melting.

ehild
 

Related to Heat problem, determine mass of ice cube?

1. What is the heat problem and why is it important to determine the mass of an ice cube?

The heat problem refers to the transfer of thermal energy from a warmer object to a cooler object. In the case of determining the mass of an ice cube, it is important because the amount of heat transferred is directly proportional to the mass of the ice cube. This means that by measuring the amount of heat transferred, we can calculate the mass of the ice cube.

2. How is the mass of an ice cube determined using the heat problem?

The mass of an ice cube can be determined using the heat problem by measuring the amount of heat (in joules) transferred from the warmer object (such as a heated metal rod) to the ice cube. This heat transfer can be measured using a calorimeter or by monitoring the temperature change of the warmer object before and after it comes into contact with the ice cube. The mass of the ice cube can then be calculated using the formula Q = mcΔT, where Q is the amount of heat transferred, m is the mass of the ice cube, c is the specific heat capacity of ice, and ΔT is the change in temperature of the warmer object.

3. What variables are involved in determining the mass of an ice cube using the heat problem?

The variables involved in determining the mass of an ice cube using the heat problem are the amount of heat transferred (Q), the specific heat capacity of ice (c), and the change in temperature of the warmer object (ΔT). These variables can be measured or calculated using appropriate equipment and techniques.

4. Are there any limitations to using the heat problem to determine the mass of an ice cube?

Yes, there are some limitations to using the heat problem to determine the mass of an ice cube. For example, this method assumes that the only heat transfer is between the warmer object and the ice cube, and that there is no heat loss to the surrounding environment. In reality, there may be other factors that can affect the accuracy of the measurement, such as the insulating properties of the container holding the ice cube. Additionally, the specific heat capacity of ice may vary slightly depending on the composition and purity of the ice cube.

5. Can the heat problem be used to determine the mass of other objects besides ice cubes?

Yes, the heat problem can be applied to determine the mass of other objects besides ice cubes. This method relies on the principle that the amount of heat transferred is directly proportional to the mass of the object. Therefore, by measuring the amount of heat transferred and knowing the specific heat capacity of the object, we can calculate its mass. This method can be applied to various objects, such as metals, liquids, and other materials.

Similar threads

I try to solve a thermodynamics problem on heat transfer
    • Introductory Physics Homework Help
Replies
3
Views
1K
How much ice to cool down this water?
    • Introductory Physics Homework Help
Replies
17
Views
3K
Calculate the Mass of Ice cubes needed to cool a soft drink
    • Introductory Physics Homework Help
Replies
10
Views
2K
Find the fractional increase in inertial mass when an ice cube melts
    • Introductory Physics Homework Help
Replies
10
Views
2K
Thermodynamics - Latent Heat Problem (finding mass)
    • Introductory Physics Homework Help
Replies
7
Views
1K
Heat question -- Ice cube in a cup of water....
    • Introductory Physics Homework Help
Replies
7
Views
8K
Solving Heat Transfer Problem with Melting Ice Cube
    • Introductory Physics Homework Help
Replies
4
Views
2K
Find the mass and side length of unknown ice cube?
    • Introductory Physics Homework Help
Replies
6
Views
1K
Question about thermal physics -- Ice cubes melting in water
    • Introductory Physics Homework Help
Replies
8
Views
2K
Mass of Ice required to achieve a certain final Temperature
    • Introductory Physics Homework Help
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top