MrMechanic
- 46
- 0
Homework Statement
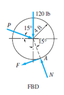
Calculate the force P that is required to hold the 120lb roller at rest on the rough incline. (see attachments for Free body diagram)
Homework Equations
Summation of Forces X = 0
Summation of Forces Y = 0
Summation of Moment along A = 0
Moment = Fd
The Attempt at a Solution
well here's what i did...
Summation of moment along A = 0 [clockwise = positive]
-4(Psin15) + 4Pcos15 - 4(120sin15) = 0
P = 4(120sin15) / 4cos15 -4sin15
P = 43.923 lb
Which is wrong.. I've found out that the correct answer is 53.6lb
Can someone explain to me? on where did I go wrong.