Help! Finding Direction of Current in Magnetic Circuit

[archaic]

Homework Statement

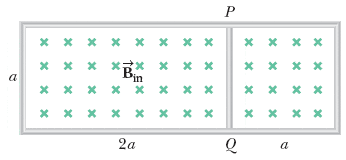
The circuit in the figure below is located in a magnetic field whose magnitude varies with time according to the expression $B=1.00\times10^{-3}t$, where $B$ is in teslas and $t$ is in seconds. Assume the resistance per length of the wire is $0.094$ Ω/m. Find the magnitude of the current in section $PQ$ of length $a = 55.0$ cm, and its direction.

Relevant Equations

$$\mathcal{E}=-\phi_B'(t)$$

I have nearly finished my homework, but am blocking at one of the simplest questions...

I'm going to let $\rho=0.094\,\Omega/m$
Since the magnetic flux is increasing, then, by Lenz's law, the current in both loops is counter-clockwise.
If we only look at the left loop, then $\phi_L=2a^2B\Leftrightarrow\mathcal{E}=-2a^2B'(t)$. The resistance is $R=6a\rho$, so $I_L=-\frac{aB'(t)}{3\rho}\approx−0.00195\,A$ (L for left).
If we only look at the right loop, then $\phi_R=a^2B\Leftrightarrow\mathcal{E}=-a^2B'(t)$. The resistance is $R=4a\rho$, so $I_R=-\frac{aB'(t)}{4\rho}\approx−0.00146\,A$.
Since $I_L$ comes to $PQ$ from $Q$, and is more negative than $I_R$, then the direction of the total current is from $Q$ to $P$, and $|I|=I_R-I_L$.
The resultant magnitude is wrong, but the direction of the current is correct. Can anyone guide me a bit? Thank you very much!

 

[Frigus]

Are all results wrong?
Have you checked if it has errata?

 

[archaic]

Are all results wrong?
Have you checked if it has errata?

Hello! I have improved my answer a bit.

The resultant magnitude is wrong, but the direction of the current is correct.

No, no errata. This is from a homework platform.

 

[Frigus]

Hello! I have improved my answer a bit.

No, no errata. This is from a homework platform.

What is answer friend?
I am also getting the same values as you.

 

[archaic]

What is answer friend?
I am also getting the same values as you.

I don't know, the due date of the HW is the 7th.

 

[TSny]

Since the magnetic flux is increasing, then, by Lenz's law, the current in both loops is counter-clockwise.
If we only look at the left loop, then $\phi_L=2a^2B\Leftrightarrow\mathcal{E}=-2a^2B'(t)$. The resistance is $R=6a\rho$, so $I_L=-\frac{aB'(t)}{3\rho}\approx−0.00195\,A$ (L for left).
If we only look at the right loop, then $\phi_R=a^2B\Leftrightarrow\mathcal{E}=-a^2B'(t)$. The resistance is $R=4a\rho$, so $I_R=-\frac{aB'(t)}{4\rho}\approx−0.00146\,A$.
Since $I_L$ comes to $PQ$ from $Q$, and is more negative than $I_R$, then the direction of the total current is from $Q$ to $P$, and $|I|=I_R-I_L$.

This method is not correct. You can't treat the left and right loops in this way. I recommend that you consider three unknown currents as shown

Set up three independent equations for the currents.

 

[archaic]

This method is not correct. You can't treat the left and right loops in this way. I recommend that you consider three unknown currents as shown
View attachment 272064

Set up three independent equations for the currents.

Hello, and thanks! Someone else also has proposed this to me.

I oriented the batteries in the same way because both emfs have the same sign, and also because the induced current is counter-clockwise in both loops. Is this the good reason?
The emfs are calculated as in my first post, and the resistances are $R=a\rho$, $R_L=5a\rho$, and $R_R=3a\rho$.
Assuming that the desired current goes from $Q$ to $P$, I get$$\begin{align*}
I&=I_L-I_R\\
I_L&=\frac{\mathcal{E}_L}{R_L}-\frac{R}{R_L}I\\
I_R&=\frac{\mathcal{E}_R}{R_R}+\frac{R}{R_R}I
\end{align*}$$$$I=\frac{\frac{\mathcal{E}_L}{R_L}-\frac{\mathcal{E}_R}{R_R}}{1+\frac{R}{R_L}+\frac{R}{R_R}}$$
I am not really sure why I would think this to be true, though. Is my treatment of the loops in the original post correct in determining the direction of the current? If not, then how do we do it?

 

[Delta2]

In post #1 I agree with the direction of currents but I disagree with the respective formulas for the calculation of $I_L$ and $I_R$. You treat them like each of them is the only current that runs through the PQ conductor, but both currents affect the current that runs through the PQ segment according to the equation you have wrote that is $I_{PQ}=I_L-I_R$
In post #7 I think the equivalent circuit is correct. But I am not sure about the last 3 equations, can you show us in more detail how you derive them?

 

[Delta2]

I now had the time to check more carefully your equations of post #7 and I think they are correct.

 

[archaic]

Hey @Delta2! Thank you very much! Sorry for not having written the entire derivation.

but both currents affect the current that runs through the PQ segment according to the equation you have wrote that is $I_{PQ}=I_L-I_R$

Ha! So my reasoning for that was correct.

I now had the time to check more carefully your equations of post #7 and I think they are correct.

Thanks again!