murrayk91
- 2
- 0
A graph of position versus time for a certain particle moving along the x-axis is shown in the figure below. Find the instantaneous velocity at the following instants.
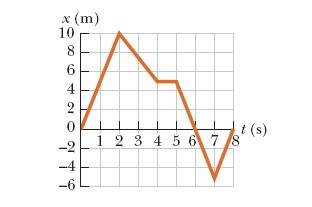
(a) t = 1.00 s
(b) t = 3.00 s
(c) t = 4.50 s
(d) t = 7.50 s
I know that a) is 5 m/s and c) is 0 m/s, but I need help figuring out b) and d). I don't understand how to draw the tangent line to find the instantaneous velocity.
For 3.00 s the answers I've come up with are wrong. I though using the slope of two points on the line, (7-10)/(3-2) should give me the answer. Any help?
(a) t = 1.00 s
(b) t = 3.00 s
(c) t = 4.50 s
(d) t = 7.50 s
I know that a) is 5 m/s and c) is 0 m/s, but I need help figuring out b) and d). I don't understand how to draw the tangent line to find the instantaneous velocity.
For 3.00 s the answers I've come up with are wrong. I though using the slope of two points on the line, (7-10)/(3-2) should give me the answer. Any help?
Last edited: