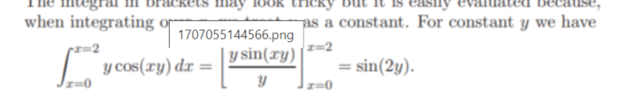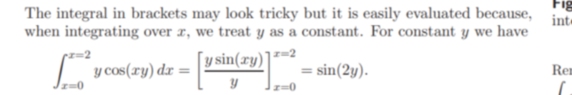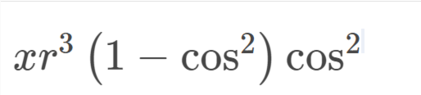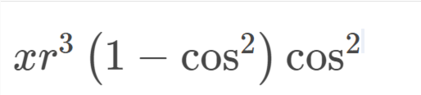Help please integrating this function over a rectangular area

[Martyn Arthur]

TL;DR

Area Integration

Hi I struggle with integration generally. Could you be able please to talk me through the stages of this one?
thanks
martyn

 

[kuruman]

Can you do the integral $$I=\int_0^2a\cos(ax)dx$$where $a=~$constant? If so, what do you get? Do you see why the resut is a function of $a$, i.e. you can write $I=f(a)$ which means "you give me a value for $a$ and I will give you a value for $I$?"

 

[Mark44]

Could you be able please to talk me through the stages of this one?

It would be helpful if you told us exactly which parts you don't understand. If your answer is "all parts," then my suggestion would be to go back to the start of the section in your textbook where iterated integration is introduced.

BTW, questions like this one normally should be posted in the Homework Help section, under Calculus & Beyond, and should include your efforts to find a solution.

 

[Martyn Arthur]

Thanks;
I did the underlying theory of integration in year one of the degree but the cross over to this second year has been difficult with little explanation.

I understand the basics of the overall thing, sin is a basic integral of cos et al.
I understand that integral 3 is integrating the second piece of the action.
I understand the maths of that calculation.
I am completely lost as to the overall mechanics of the conversion of sin to (-1/2cos).
Given that integral 2 produces a conclusion how do they fit together.
To try to make myself clear its the process that confuses me.
thanks
martyn

 

[Martyn Arthur]

By reference to Mark44 thanks,
I take the point about homework which I note.
I hope my later post makes my problem more clear..
There is no adequate crossover in the text from the integration procedures which I understand to the practical application that is now produced.
I think some gentle support on the "bits" of a couple of points will see me through to a fuller understanding.

 

[Mark44]

I am completely lost as to the overall mechanics of the conversion of sin to (-1/2cos).

This integral is $$\int_{x=\pi/2}^\pi \sin(2y)~dy$$
Integration here is pretty straightforward, using a substitution; namely u = 2y, so du = 2dy, so dy = 1/2 du. This produces the (indefinite) integral $\int \sin(u)~ (1/2) du$.
Can you evaluate that one?

Given that integral 2 produces a conclusion how do they fit together.

Integral 2 is not the conclusion. It is the result of the integral in parentheses in integral 1.

 

[PeroK]

I am completely lost as to the overall mechanics of the conversion of sin to (-1/2cos).

I suspect at this level you are expected to recognise a common anti-derivative like this.

 

[Martyn Arthur]

Fair comment; working on it

 

[Martyn Arthur]

You guys are so patient. Given the following
xr^3(1-cos^2θ)cos^2θ
I need to make the substitution u = (1-cos^2θ) have I got it right?
Thanks

 

[Mark44]

You guys are so patient. Given the following
xr^3(1-cos^2θ)cos^2θ
I need to make the substitution u = (1-cos^2θ) have I got it right?
Thanks
View attachment 340095

I can't make any sense of this of the attachments. They are the same image double-posted and are as follows:
$$xr^3(1 - \cos^2)(\cos^2)$$
What does this mean? Why is $\theta$ missing from the attachments?
What are you supposed to do with this?

The work you show also makes little sense, partly because some of it is cut off, partly because it's hard to decipher, and partly because much of the rest doesn't make sense.

At the top you have "Let $u = (1 - \cos^2\theta)$" and then <something> u = $\cos u$ <something>
In the 2nd equation on the left side you have a squiggle -- is it f? Or is it an integral sign? On the right side the top of the fraction is cut off. Is where I have ? supposed to be d?

On the next line you have $\frac d {d\theta} = -\cos^2 \theta$

This doesn't make sense for a couple of reasons:

1) On the left side you have a differentiation operator, but are missing whatever it is that you are differentiating? Should this have been $\frac{du}{d\theta}$?

2)Assuming that you meant $\frac{du}{d\theta}$ on the left side of the second line, the right side is not the derivative of $1 - \cos^2\theta$

If the goal is to find the derivative of $1 - \cos^2 \theta$, your answer at the bottom is correct, but there is a lot of cruft and incorrect stuff along the way.

Note that $1 - \cos^2 (\theta) = \sin^2(\theta)$ so

$\frac d {d\theta}(1 - \cos^2 (\theta)) = \frac d {d\theta}(\sin^2(\theta)) = 2\sin(\theta) \cdot \frac d {d\theta} (\sin(\theta)) = 2\sin(\theta) \cdot \cos(\theta) = \sin(2\theta)$

 

[Mark44]

Thread closed. @Martyn Arthur, since this is a new problem, please start a new thread. The appropriate place for it is the Homework Help section, under Calculus and Beyond.