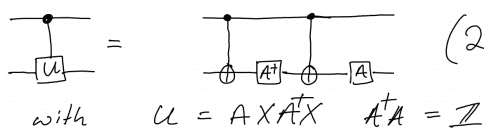SUMMARY
The discussion centers on the quantum circuit identity for converting a controlled U gate into a series of CNOT gates and single qubit gates, represented by the equation U = AXA†X, where A is a unitary matrix. Participants emphasize the practicality of using simpler single qubit operations and CNOT gates instead of directly implementing the controlled U gate. The identity allows for the transformation of a 4x4 controlled U matrix into a combination of two CNOTs and two single-qubit operations, maintaining the same quantum state. Understanding the definition of the unitary matrix A is crucial for achieving the desired outcome with the controlled U gate.
PREREQUISITES
- Quantum mechanics fundamentals
- Understanding of unitary matrices
- Familiarity with CNOT gates
- Basic knowledge of quantum circuit design
NEXT STEPS
- Study the properties of unitary matrices in quantum mechanics
- Learn about the implementation of CNOT gates in quantum circuits
- Explore the derivation and applications of controlled gates in quantum computing
- Investigate the use of single-qubit operations in quantum algorithms
USEFUL FOR
Quantum computing enthusiasts, researchers in quantum mechanics, and practitioners designing quantum circuits who seek to optimize the implementation of controlled gates using simpler operations.