Help with determining distance where electric potential is 0

AI Thread Summary
The discussion focuses on determining the distance from a +4.0 nC charge to a point where the electric potential is zero. The user initially applies the formula for electric potential and sets the sum of potentials from two charges to zero. They encounter difficulty in solving the resulting equation involving fractions. After some back-and-forth, the user successfully resolves the problem. The thread highlights the process of setting up the equation and the challenges in solving it.
Hannah7h
Messages
39
Reaction score
0
Member advised to use the homework template for posts in the homework sections of PF.
Question states 'Determine the distance from the +4.0nC charge to the point, along the straight line between the charges, where the electric potential is zero.'

upload_2016-5-29_16-5-50.png


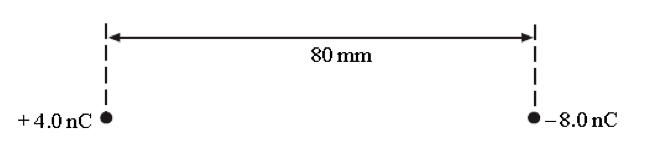
This is as far as I've got: so I've used V=Q/4pi(epsilon0)r and then set it so V1+V2=0 (to find the point where the resultant electric potential is zero). Then the 4pi(epsilon0) can just be ignored as it is a constant, therefore V1=Q1/R1 and then V2=Q2/R2 therefore Q1/R1 + Q2/R2 = 0 so then (substituting in the values), 4x10^-9/r - 8x10^-9/ (80x10^-3) -r = 0 AND now I'm not sure where to go from this point

Thank you for any help
 
Physics news on Phys.org
do the sum between fractions and solve the equation in ##r## ...
 
Ssnow said:
do the sum between fractions and solve the equation in ##r## ...

yeah that's the bit I can't seem to do my answer keeps coming out at 7000
 
Ssnow said:
do the sum between fractions and solve the equation in ##r## ...

No worries I've got it now thanks!
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Electromagnetism problem: Merging of 2 charged drops of mercury
Replies
2
Views
1K
What is taken as datum level for the following absolute potentials?
Replies
2
Views
558
Electric potential due to collection of charged particles
Replies
3
Views
2K
Find the electric field between 2 finite discs
Replies
16
Views
1K
Change in electric potential energy
Replies
3
Views
2K
Electric potential inside a shell of charge
Replies
3
Views
2K
At what point is Electric Potential zero
Replies
2
Views
2K
Electric Potential Problem - Fixed Template
Replies
2
Views
1K
MIT OCW, 8.02 Electromagnetism: Potential for an Electric Dipole
Replies
1
Views
2K
Potential of a spherical shell
Replies
7
Views
5K

Hot Threads

Recent Insights

Back
Top