Hazy001
- 2
- 0
Member warned about not using the homework template
f(x) =
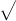 3x^3 + 3x^2+ 2x + 1
3x^3 + 3x^2+ 2x + 1
,a = 3
formal is
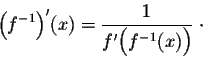
Homework is due tonight and this is the only problem i can't solve
Your suppose to
3=
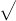 3x^3 + 3x^2 + 2x + 1
3x^3 + 3x^2 + 2x + 1
, solve for xThe find the derivative of y=
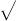 3x^3 + 3x^2 + 2x + 1
3x^3 + 3x^2 + 2x + 1
, then plug x into that and put it under 1.
,a = 3
formal is
Homework is due tonight and this is the only problem i can't solve
Your suppose to
3=
, solve for xThe find the derivative of y=
, then plug x into that and put it under 1.