nn2e19
- 1
- 0
Hello,
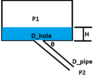
I want to size my system to be able to get rid of fluids without any head buildup within the container. I am just a bit confused as to what formula I should use. My problem is summed up in the following schematic. Note that P1>P2, I have assumed H=10^(-4)m and my flow rate is 0.1 m3/s, dynamic viscosity is 10^(-3) Pa.s. the pipe length is 3.2m. I do not really care about the numbers, I just want to be sure the methodology is correct.
If I use the Bernoulli eqn to size D_hole I use this: Q = Cd*Area*sqrt(2*(g*H+dP/rho)), Area = pi*D_hole^2/4
If I use the same dP and flowrate to get D_pipe I use Q = ((dP-rho*g*L*sin(theta)*pi*D^4)/(128μL))
I'm just baffled as to which one is more suitable for my problem.
Any help is greatly appreciated.
I want to size my system to be able to get rid of fluids without any head buildup within the container. I am just a bit confused as to what formula I should use. My problem is summed up in the following schematic. Note that P1>P2, I have assumed H=10^(-4)m and my flow rate is 0.1 m3/s, dynamic viscosity is 10^(-3) Pa.s. the pipe length is 3.2m. I do not really care about the numbers, I just want to be sure the methodology is correct.
If I use the Bernoulli eqn to size D_hole I use this: Q = Cd*Area*sqrt(2*(g*H+dP/rho)), Area = pi*D_hole^2/4
If I use the same dP and flowrate to get D_pipe I use Q = ((dP-rho*g*L*sin(theta)*pi*D^4)/(128μL))
I'm just baffled as to which one is more suitable for my problem.
Any help is greatly appreciated.