Horizontal force kinematics help

[frozen7]

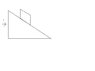
The figure shows a small object of mass m = 1kg can slide without friction on a wedge of mass M = 3kg inclined at angle \delta=30 degree . What horizontal force F must be applied to the wedge if the small block is not to move with respect to the wedge?

I do it in this way:

By Newton`s 3rd law: the small object will exert a same force F to the wedge, so

mgsin30 = Fcos30
F = 5.66N

But my answer is wrong. Can anyone teach me how to solve it?
Thanks.

 

[stunner5000pt]

mg sin 30 = F
no Fcos30 coz you're applying this force in the same direction as the slant.

 

[Fermat]

I've got an idea for the solution of this problem, but I'm not sure how feasible it is

The small mass is moving on a smooth surface, so there is no friction.
The accelerating force down the slope is mg.sin@ (where @ is the slope of the wedge). So the acceln of the mass down the slope is a=g.sin@.
The mass has a horizontal acceleration of a_h = a.cos@ = g.sin@.cos@ = ½g.sin(2@).

My idea: If the wedge is now moved forward with a horizontal acceleration of a_h, equal to that of the small mass, then this will provide vertical support for the small mass such that no vertical movement of it will happen and it will be motionless wrt the wedge.

Any comments on my idea ??

Assuming my idea is correct,

F = (m+M)a_h
F = (m+M).½g.sin(2@).
F = ½g.(m+M).sin(2@).
=================

F = 4.9*(1 + 3)*sin(60)
F = 16.974 N
==========

 

[frozen7]

There are 4 choices answers for this question:
a)22.6
b)28.4
c)32.5
d)36.2

 

[mukundpa]

If it is not sliding m is also accelerating with the same acceleration.

Draw a free body diagram of object m resolve the forces in horizontal and vertical direction and you will get acceleration probably g tan(theta).

 

[frozen7]

But, is this relation correct?

mgsin30 = Fcos30

Furthermore, can you explain to me about the free body diagram? I can't see why a = g tan(theta)

Thanks.

 

[mukundpa]

Free body diagram mens the diagram showing all forces acting on a single body. For m it is in the attaqchment.

 

[mukundpa]

As m is not in equlibrium N is not equal to mg cos@.

 

[frozen7]

Mukundpa...Thanks a LOT...

 

[mukundpa]

You are always Welcome