velo city
- 26
- 0
I have attached the image as an attachment
I am reading a classical mechanics textbook and I don't understand how they found that.
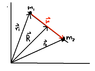
r1' = -\frac{m_{2}}{m_{1}+m_{2}}r
and
r2' = \frac{m_{1}}{m_{1}+m_{2}}r
r1' is the vector from the center of mass R to m1 and r2' is the vector from the center of mass R to m2.
Center of mass = \frac{m_{1}r_{1}+m_{2}r_{2}}{m_{1}+m_{2}}
Homework Statement
I am reading a classical mechanics textbook and I don't understand how they found that.
r1' = -\frac{m_{2}}{m_{1}+m_{2}}r
and
r2' = \frac{m_{1}}{m_{1}+m_{2}}r
r1' is the vector from the center of mass R to m1 and r2' is the vector from the center of mass R to m2.
Homework Equations
Center of mass = \frac{m_{1}r_{1}+m_{2}r_{2}}{m_{1}+m_{2}}