How Do Electrons Focus When Emitted from a Cylinder?

[Saitama]

Homework Statement

(see attachment 1)

Homework Equations

The Attempt at a Solution

Here's what I've thought.
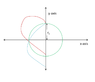
See attachment 2. I think that the emitted electrons will follow trajectories which would intersect at a common point. The differently coloured trajectories shows different trajectories for emitted electrons.

I am having trouble making equations now. I just don't know where to start from.
The centrifugal force is balanced by the attractive force due to the electric field of cylinder. This is for the electron emitted exactly to the left.
\frac{mv_0^2}{r_0}=eE
where E is the electric field due to long cylinder.
v_0^2=\frac{eEr_0}{m}
This speed is same for all the emitted electrons as per the question.

Any help is appreciated. Thanks!

 

[mfb]

First, I would get rid of prefactors, and express everything relative to r₀, v₀ and so on.

Afterwards, can you write down the equation of motion (as differential equation)? For r close to r₀, r' close to 0 and so on, you can approximate this (it might be useful to write the radius as 1+deltar_r or similar), and get a differential equation which is easy to solve afterwards.

 

[Saitama]

First, I would get rid of prefactors, and express everything relative to r₀, v₀ and so on.

Afterwards, can you write down the equation of motion (as differential equation)? For r close to r₀, r' close to 0 and so on, you can approximate this (it might be useful to write the radius as 1+deltar_r or similar), and get a differential equation which is easy to solve afterwards.

Sorry mfb but I am still not sure what to do. How do I write the differential equation? A few more hints would help.

 

[mfb]

How do I write the differential equation?

Which forces are acting on the electron? With F=m*a, you can convert this to a differential equation. Polar coordinates can be useful.

 

[Saitama]

Which forces are acting on the electron? With F=m*a, you can convert this to a differential equation. Polar coordinates can be useful.

I was expecting that I would have to use Polar coordinates here but I am not much familiar with them. See the attachment .

The forces acting on the electron are centrifugal force and force due to electric field of cylinder.
I can't calculate the centrifugal force as I don't know the radius of curvature. Is it simply r? :(

The velocity vector is tangent to the trajectory. How do I calculate $\phi$ in terms of $\theta$?

 

[mfb]

I am sure there are formulas for motion in polar coordinates somewhere.

How do I calculate ϕ in terms of θ?

That will be the result of the differential equation.

 

[Saitama]

I am sure there are formulas for motion in polar coordinates somewhere.
That will be the result of the differential equation.

To form the differential equation, I need to know the centrifugal force. I still don't know how would I calculate the radius of curvature.

I don't know the formulas you are talking about. Can you pass on a link for that?

 

[mfb]

Centrifugal force is a fictious force, you don't have to include it if you don't work with a rotating coordinate system. Otherwise, the radius is just the current radius (coordinate) of the object, and pointing in radial direction.

I don't know the formulas you are talking about. Can you pass on a link for that?

I would have to search (or derive) them as well, and it is not my homework question.

 

[Saitama]

Centrifugal force is a fictious force, you don't have to include it if you don't work with a rotating coordinate system. Otherwise, the radius is just the current radius (coordinate) of the object, and pointing in radial direction.

Are these equations fine?
m\frac{dv_x}{dt}=eE\sin\theta
m\frac{dv_y}{dt}=eE\cos\theta

where $v_x=v\cos\phi$ and $v_y=v\sin\phi$

 

[mfb]

I would expect some r-dependence of the force...
And those coefficients can be removed.

 

[Saitama]

I would expect some r-dependence of the force...

Yes, the force is inversely proportional to r.
The expression for $v_0^2$ can be rewritten as
v_0^2=\frac{eEr_0}{m}=\frac{er_0}{m}\cdot\frac{\lambda}{2\pi\epsilon_0 r_0}=\frac{e\lambda}{2\pi m \epsilon_0}

where $\lambda$ is the linear charge density of thin cylinder (which can be approximated to a infinite long wire)

The differential equations can be written as
\frac{dv_x}{dt}=\frac{v_0^2}{r}\sin\theta
Replacing $v_x$ with $v\cos\phi$
\cos\phi\cdot\frac{dv}{dt}-v\sin\phi\frac{d\phi}{dt}=\frac{v_0^2}{r}\sin\theta
\Rightarrow \frac{dv}{dt}-v\tan\phi\frac{d\phi}{dt}=\frac{v_0^2}{r}\cdot\frac{\sin\theta}{\cos \phi}

Similarly the second differential equation can be simplified to
\frac{dv}{dt}+v\cot\phi\frac{d\phi}{dt}=\frac{v_0^2}{r}\cdot\frac{\cos \theta}{\sin\phi}

Am I in the right direction?

 

[mfb]

Your definition of angles looks confusing. I would not introduce ϕ at all, I don't see how it helps. v_x, v_y are fine, you can convert them to r', θ' afterwards.

 

[Saitama]

Your definition of angles looks confusing. I would not introduce ϕ at all, I don't see how it helps. v_x, v_y are fine, you can convert them to r', θ' afterwards.

I still don't know what to do. Considering the differential equation,
\frac{dv_x}{dt}=\frac{v_0^2}{r}\sin\theta
I have four variables, what should I do?

 

[mfb]

You can write v_x in terms of r and θ and their derivatives. You get a similar equation for the y-component, which gives you two equations for two unknown parameters (r and θ as function of t). Afterwards, you can start using approximations to simplify the equations.

 

[Saitama]

You can write v_x in terms of r and θ and their derivatives. You get a similar equation for the y-component, which gives you two equations for two unknown parameters (r and θ as function of t). Afterwards, you can start using approximations to simplify the equations.

I can write $\displaystyle v=r\frac{d\theta}{dt}$ but how would I write v_x in terms of r and θ?
You said me not to introduce $\phi$ so I am utterly confused about expressing v_x in r and θ. Sorry if I am missing out something obvious.

Is v_x=vcosθ?

 

[mfb]

Express the position (x,y) as function of r and θ, v_x is just the derivative of the x-coordinate in time.
You don't need that detour at all, if you start with the coordinates itself and not with v_x and v_y.

Is v_x=vcosθ?

No.

 

[Saitama]

Express the position (x,y) as function of r and θ, v_x is just the derivative of the x-coordinate in time.
You don't need that detour at all, if you start with the coordinates itself and not with v_x and v_y.

$x=r\sin\theta$
$y=r\cos\theta$

v_x=\frac{dx}{dt}=\sin\theta \frac{dr}{dt}+r\cos\theta \frac{d\theta}{dt}
v_y=\frac{dy}{dt}=\cos\theta \frac{dr}{dt}-r\sin\theta \frac{d\theta}{dt}

Should I use these two relations: $v^2=v_x^2+v_y^2$ and $v=r\frac{d\theta}{dt}$?

 

[mfb]

That could give interesting results, but I don't know how exactly you plan to use them. The formula for v= is wrong (r is not constant).

 

[Saitama]

That could give interesting results, but I don't know how exactly you plan to use them. The formula for v= is wrong (r is not constant).

I am stuck again. :(
If I plug in the expressions for v_x and v_y in v^2=v_x^2+v_y^2, I end up with
v^2=\left(\frac{dr}{dt}\right)^2+r^2\left(\frac{d\theta}{dt}\right)^2

 

[Saitama]

Can you please help me further? :)

 

[mfb]

Okay, as I lost the overview over all those formulas, I give you some approach to begin:

First, define $v'=\frac{v}{v_0}$, $r'=\frac{r}{r_0}$ and $F'=\frac{F}{m}$, and drop the ' afterwards.Therefore, the initial conditions are v=1, r=1. The force is proportional to 1/r and it is 1 at r=1. Therefore, it can be written as $\ddot{\vec{r}}=F(r)=\frac{\vec{r}}{r^2}$.

Now you can plug in a vector (x,y) in $\vec{r}$, and get equations $\ddot{x}=$, $\ddot{y}=$.

At the same time, you know that $r^2=x^2+y^2$. You can calculate the second derivative in time of that expression (just modify the right side, the left side is fine). This leads to an expression where the second derivative of r^2 depends on the velocity (and constants) only.

Spoiler

The velocity is a function of the radius only. You can express v in terms of r, where an approximation ($r\approx1$) is useful. Finally, you can solve the differential equation to get an oscillation period.

 

[Saitama]

Okay, as I lost the overview over all those formulas, I give you some approach to begin:

First, define $v'=\frac{v}{v_0}$, $r'=\frac{r}{r_0}$ and $F'=\frac{F}{m}$, and drop the ' afterwards.Therefore, the initial conditions are v=1, r=1. The force is proportional to 1/r and it is 1 at r=1. Therefore, it can be written as $\ddot{\vec{r}}=F(r)=\frac{\vec{r}}{r^2}$.

Now you can plug in a vector (x,y) in $\vec{r}$, and get equations $\ddot{x}=$, $\ddot{y}=$.

At the same time, you know that $r^2=x^2+y^2$. You can calculate the second derivative in time of that expression (just modify the right side, the left side is fine). This leads to an expression where the second derivative of r^2 depends on the velocity (and constants) only.

Spoiler

The velocity is a function of the radius only. You can express v in terms of r, where an approximation ($r\approx1$) is useful. Finally, you can solve the differential equation to get an oscillation period.

\ddot{x}=\frac{x}{x^2+y^2}
\ddot{y}=\frac{x}{x^2+y^2}

Differentiating the equation of circle.
r^2 \frac{d^2r}{dt^2}+\left( \frac{dr}{dt} \right)^2=x \frac{d^2x}{dt^2}+ \left( \frac{dx}{dt} \right)^2 +y \frac{d^2y}{dt^2}+ \left( \frac{dy}{dt} \right)^2
Substituting the expressions for $\ddot{x}$ and $\ddot{y}$,
r^2\frac{d^2r}{dt^2}+\left(\frac{dr}{dt}\right)^2=\frac{x^2}{x^2+y^2}+ \frac{y^2}{x^2+y^2}+v^2
r^2\frac{d^2r}{dt^2}+\left(\frac{dr}{dt}\right)^2=1+v^2

What's next?

 

[ehild]

Pranav, use polar coordinates. http://www.ecourses.ou.edu/cgi-bin/ebook.cgi?doc=&topic=dy&chap_sec=01.6&page=theory

You see that the acceleration of the electron has a radial and an azimuthal component. As the force is radial (central force) the azimuthal component of the acceleration is zero. That is equivalent to the law of conservation of angular momentum in case of central forces.

The problem asks the position of the focal point in terms of the angle. Consider the radius r as function of the angle θ, and write the time derivatives of r in terms of θ and dθ/dt.

That is enough for the time being.

ehild

 

[Saitama]

The problem asks the position of the focal point in terms of the angle. Consider the radius r as function of the angle θ, and write the time derivatives of r in terms of θ and dθ/dt.

And how will I do that? I have no idea how will I express r in terms of θ and its derivative. :(

 

[ehild]

Apply chain rule. The radius is function of θ and θ is function of the time. The time derivatives of r can be expressed by the derivatives with respect to θ and the time derivatives of θ.

dr(θ(t))/dt = dr/dθ dθ/dt...

ehild

 

[Saitama]

Apply chain rule. The radius is function of θ and θ is function of the time. The time derivatives of r can be expressed by the derivatives with respect to θ and the time derivatives of θ.

dr(θ(t))/dt = dr/dθ dθ/dt...

ehild

I know that if I differentiate r(θ(t)) I have to apply chain rule but you asked me the function r(θ(t)) and I don't know how those derivative would help.

Do I have to substitute expressions for dr/dθ and dθ/dt?

 

[ehild]

From Newton's II you get an equation for vector r(t). In polar coordinates, that yields two differential equations for the the radius r and the angle θ as functions of time. You need to solve them, applying also the initial condition.
One equation can be easily solved, and the solution is equivalent to the conservation of angular momentum: r²dθ/dt=const.

The electron orbits around the axis of the cylinder in the xy plane. You can write up the trajectory as function of the angle. So it is useful to express the time derivatives of r with the derivatives with respect to θ.
At the end you get a differential equation for r(θ), and you need the approximate solutions when the trajectory does not differ much from a circle.
I also sent you a pm.

ehild

 

[mfb]

What's next?

The left side can be written as $\ddot{r^2}$, and the next hint is hidden in the spoiler.
With the approximation of small deviations from r=1, you can get a differential equation of the type $\ddot{\Delta r} = -k \Delta r$.