Understanding Spherical Symmetry of Electron Clouds in External Fields

[versine]

Homework Statement

A hydrogen atom consists of a proton nucleus of charge +e and an electron of charge -e. The charge distribution of the atom is spherically symmetric, so the atom is nonpolar. Consider a model in which the hydrogen atom consists of a positive point charge +e at the center of a uniformly charged spherical cloud of radius R and total charge -e. Show when an atom is placed in a uniform external electric field vector E, the induced dipole moment is proportional to vector E; that is vector p = alpha * vector E, where alpha is called the polarizability.

Relevant Equations

Electric Dipole
Coulomb law
Shell Theorem

The given diagram looks something like this:

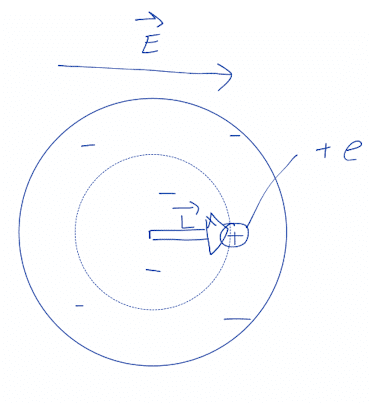
Electric force on nucleus from external field must balance attraction force from electron cloud and electric force from external field.

$$e\vec{E}=\frac{k(\frac{L^3}{R^3}e)}{L^2}\hat{L}$$ where $\vec{L}$ is from center of electron cloud to nucleus.

$$\vec{E}=\frac{keL\hat{L}}{R^3}=\frac{k\vec{p}}{R^3}\implies\vec{p}=4\pi\epsilon_0R^3\vec{E}$$

But why can you treat the electron cloud as a spherically symmetric charge distribution even after the external electric field is applied? The external electric field will repel it. Shouldn't it be more of an oval shape, with the charge distribution more concentrated near the new location of the nucleus?

 

[hutchphd]

The problem simply asks you to assume that the distribution of charge of the electron remains uniform and symmetric. Of course it really isn't uniform and it doesn't remain exactly symmetric so there are two issues. For small external fields (what does small mean?) this is not a bad assumption and provides the method by which we build a better solution (using perturbation theory and quantum mechanics). But its a good question and the answer is that the real problem is difficult but these approximations work well enough often.