How Do Forces Distribute in a Block and Tackle System?

  • Thread starter Thread starter ksle82
  • Start date Start date
  • Tags Tags
    Block System
AI Thread Summary
In a block and tackle system, the forces at various points can be calculated based on the weight being lifted. The user provided specific force values for points in the system, suggesting that point 1 has a force of 40, point 2 has 20, point 3 has 20, and point 4 has 10. There is a discussion about the mechanical advantage of the system, with clarification that a 10 unit weight can lift a 20 unit weight at point 2, indicating that mechanical advantage does exist. The conversation emphasizes the importance of force balance in analyzing the system's efficiency.
ksle82
Messages
30
Reaction score
0
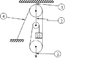
Given a block and tackle system and a known weigt, give the magnitude of the forces at the numbered points. [see attached for figure]
https://www.physicsforums.com/attachment.php?attachmentid=7026&stc=1&d=1149034106
blocktackle.JPG

My answers:
Point 2: 20
Point 3: 20
Point 4: 10
Point 1: 40

I arrived at the answers simply by looking at the figure and do a force balance at each tackle. I think some (if not all) are wrong because the systems doesn't provide any mechanical advantage (according to my answers). Please Help.
 

Attachments

  • blocktackle.JPG
    blocktackle.JPG
    15.5 KB · Views: 821
Physics news on Phys.org
Looks OK to me (assuming all ropes are essentially vertical). Why do you say there's no mechanical advantage? A 10 unit weight (shown) lifts a 20 unit weight (that's point 2).
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

How much force does the 20 kg block exert on the 10 kg block?
Replies
17
Views
2K
Distribution of Energy when work is done on a system of 2 masses connected by a spring
Replies
17
Views
2K
Block on slope. Different answers using energy vs forces
Replies
5
Views
882
Pulley system problem: 6 Pulleys and 1 Mass
Replies
5
Views
918
Time period of SHM & Energy conservation in pulley-spring-block system
Replies
24
Views
3K
Pulley rotational speed in block and tackle
Replies
3
Views
7K
Find the force so that all blocks are at rest with respect to each other
Replies
20
Views
2K
Block connected to 2 real pulleys
Replies
18
Views
804
External force on three blocks stacked
Replies
3
Views
6K
Magnitude of Force Exerted on Middle Block in a Three-Block System
Replies
14
Views
4K

Hot Threads

Recent Insights

Back
Top