- #1
jonathanM111
How do I calculate masses predicted by the force law equation
Click For Summary
Homework Help Overview
The discussion revolves around calculating theoretical values for mass differences using a force law equation, specifically in the context of an experiment involving magnetic forces. Participants are exploring how to interpret the relationship between mass and distance in their data analysis.
Discussion Character
- Exploratory, Conceptual clarification, Assumption checking
Approaches and Questions Raised
- Participants discuss the need to plot logarithmic values of mass against distance, questioning the precision of their measurements and the implications of the force law being proportional to distance cubed. There are attempts to reconcile experimental data with theoretical predictions and discussions about the appropriateness of the dipole model.
Discussion Status
The conversation is ongoing, with participants providing insights into potential approaches for plotting their data. Some suggest that the original problem may be flawed, while others are exploring different interpretations of the force law and its implications for their results.
Contextual Notes
There are mentions of the limitations of the experimental setup, including concerns about measurement precision and the assumptions underlying the dipole model. Participants are also considering the effects of the physical configuration of the magnets on their results.
- #2
- 42,892
- 10,526
https://www.physicsforums.com/conversations/locked-brainly-thread.131039/goto/post?id=5833956#post-5833956
I posted the question here on brainly https://brainly.com/question/4998386
first 3 attachments are the laboratory manual and the 4th is my attempt.
I wrote this response to your original thread, but it got locked before I could post...
I don't understand the directions you are given. Seems to me you should be plotting the log of the mass difference against the log of the distance.
Looks like you needed more precision in the mass measurements. The first half of your datapoints are useless because the mass difference is beyond the precision limit.
To answer your question, you need to compute the force predicted by the quoted law and infer the mass difference from that. However, the quoted law only specifies "is proportional to" so there will be an unknown constant factor. Since you are taking logs, that will show up on the graph as an unknown vertical displacement. This means you should slide the predicted line vertically to get the best fit with the plotted line from the measurements
I posted the question here on brainly https://brainly.com/question/4998386
first 3 attachments are the laboratory manual and the 4th is my attempt.
I wrote this response to your original thread, but it got locked before I could post...
I don't understand the directions you are given. Seems to me you should be plotting the log of the mass difference against the log of the distance.
Looks like you needed more precision in the mass measurements. The first half of your datapoints are useless because the mass difference is beyond the precision limit.
To answer your question, you need to compute the force predicted by the quoted law and infer the mass difference from that. However, the quoted law only specifies "is proportional to" so there will be an unknown constant factor. Since you are taking logs, that will show up on the graph as an unknown vertical displacement. This means you should slide the predicted line vertically to get the best fit with the plotted line from the measurements
- #3
jonathanM111
hmm, you see, I was thinking the same but I can't seem to find a way to use the formula provided, I might be misunderstanding it but I've also looked up the equation Fαd-3 but I just can't find it anywhere. Finding the new data for the plot that's proportional to the log of mass vs distance is where I am stuck.haruspex said:
- #4
- 42,892
- 10,526
You mean F∝d-3, right? This looks like a dipole equation. This is because a bar magnet is effectively made of little dipoles all pointing the same way. See https://en.m.wikipedia.org/wiki/Force_between_magnets.jonathanM111 said:
This means mg=F=kd-3 for some unknown constant k.
Trust me, reinterpret the problem as plotting log(m) against log(d).
If you take logs of both sides of this equation, what do you get?
- #5
jonathanM111
okay so I think I figured it out F is proportional to the inverse distance cubed, that's what the expression says. Therefore I can calculate the the inverse of the distance cubed and take the log from it, if I plot this new line on the graph that I have they're pretty similar in terms of their slope, which is the dipole force.haruspex said:
- #6
- 42,892
- 10,526
Ok, but please try plotting each against log(distance) instead of against distance.jonathanM111 said:
- #7
jonathanM111
this is how the two graphs look(theres more tables in this experiment) it does look correct how you say, why would the manual say otherwise?haruspex said:
- #8
jonathanM111
BTW I apologize for my sloppiness.haruspex said:
- #9
- 42,892
- 10,526
As you can see, the d-3 line is now dead straight. This is why I thought log(d) is the right way. But, interestingly, the curves from the experiment look less convincing now. Either this is down to experimental error or the exact equation to match the experiment is not F∝d-3.jonathanM111 said:
I think I see reasons it won't be quite that. For one thing, the far end of the horizontal magnet will have some effect. I'll get back to you.
- #10
jonathanM111
hmm, for your reference this is how they look they they're against plain distance.haruspex said:
- #11
- 42,892
- 10,526
Having looked into this some more, I suspect the whole question is flawed.
The dipole formula is an approximation which can be used when the lengths of the magnets are small compared with the distance between them, and even then assumes the magnets are end-to-end.
In the present case, it would be more accurate to treat the magnets as having a magnetic monopole at each end. This is still an approximation (the "Gilbert model"), but should work better here.
Unfortunately the vertical force equation gets quite messy, but to a first approximation it would be proportional to d-2, not d-3. Note that if you ignore your measurements with the largest d values the slope of the log-log graph is -2, or even a bit less.
The dipole formula is an approximation which can be used when the lengths of the magnets are small compared with the distance between them, and even then assumes the magnets are end-to-end.
In the present case, it would be more accurate to treat the magnets as having a magnetic monopole at each end. This is still an approximation (the "Gilbert model"), but should work better here.
Unfortunately the vertical force equation gets quite messy, but to a first approximation it would be proportional to d-2, not d-3. Note that if you ignore your measurements with the largest d values the slope of the log-log graph is -2, or even a bit less.
- #12
- 42,892
- 10,526
Treating each magnet as consisting of a point magnetic "charge" (i.e. monopole) at each end, I obtained an expression for the force.
The image below shows the expression [as the Excel formula, 1/A2/A2-1/(1+A2)^2-A2/(1+A2*A2)^1.5+(1+A2)/(1+(1+A2)^2)^1.5], and a graph of ln(F*L^2) against ln(d/L), where L is the length of each magnet and d is the separation between their closest poles.
It exhibits a curvature similar to the one that you plotted from measurements. The straight line fit has a gradient closer to -2 than to -3.
For larger values of d/L the gradient steepens, with no obvious limit. I believe this is because the far pole of the horizontal magnet becomes significant, rapidly weakening the force as it counteracts the force on the near end.
For very small values of d/L it should converge to -2.
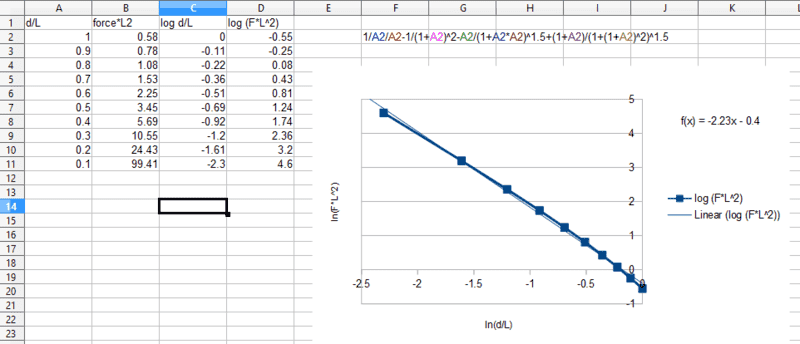
To get the d-3 relationship, the vertical magnet should be short compared with d, making it a simple dipole, but the horizontal magnet long compared with d, making it more like a monopole.
The image below shows the expression [as the Excel formula, 1/A2/A2-1/(1+A2)^2-A2/(1+A2*A2)^1.5+(1+A2)/(1+(1+A2)^2)^1.5], and a graph of ln(F*L^2) against ln(d/L), where L is the length of each magnet and d is the separation between their closest poles.
It exhibits a curvature similar to the one that you plotted from measurements. The straight line fit has a gradient closer to -2 than to -3.
For larger values of d/L the gradient steepens, with no obvious limit. I believe this is because the far pole of the horizontal magnet becomes significant, rapidly weakening the force as it counteracts the force on the near end.
For very small values of d/L it should converge to -2.
To get the d-3 relationship, the vertical magnet should be short compared with d, making it a simple dipole, but the horizontal magnet long compared with d, making it more like a monopole.