osob
- 7
- 0
Hi everyone,
I need steps and some guidance on how to solve questions like this. I know how to do right triangle questions using the Pythagorean method, but when it comes to these non right angle triangles I get so confused. Help!
1. Homework Statement
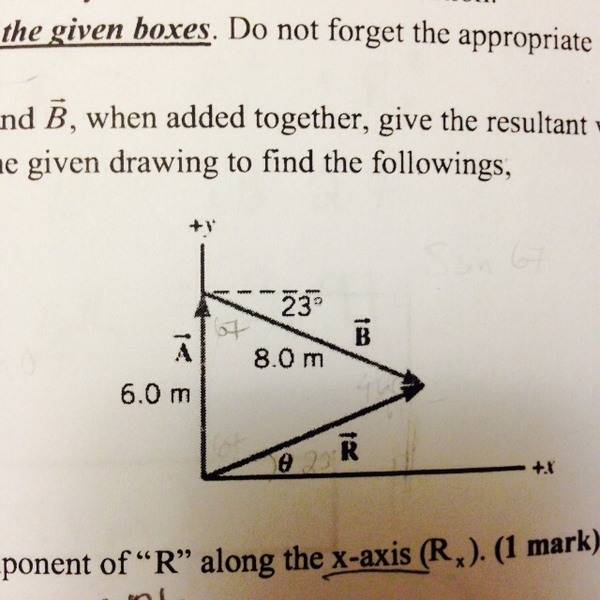
a) The magnitude of the component "R" along the x-axis?
b) The magnitude of the component "R" along the y-axis?
c) The magnitude of the resultant "R" ?
d) The direction of the resultant "R" represented by the angle it makes with the x-axis?
I don't know if I'm on the right track..
a) 8cos23= 7.36 m
b) 6sin23= 2.34 m
c) R^2 = a^2 + b^2 - 2abcos23 = 12.24 m
d) I have no clue where to begin ..
I need steps and some guidance on how to solve questions like this. I know how to do right triangle questions using the Pythagorean method, but when it comes to these non right angle triangles I get so confused. Help!
1. Homework Statement
Homework Equations
a) The magnitude of the component "R" along the x-axis?
b) The magnitude of the component "R" along the y-axis?
c) The magnitude of the resultant "R" ?
d) The direction of the resultant "R" represented by the angle it makes with the x-axis?
The Attempt at a Solution
I don't know if I'm on the right track..
a) 8cos23= 7.36 m
b) 6sin23= 2.34 m
c) R^2 = a^2 + b^2 - 2abcos23 = 12.24 m
d) I have no clue where to begin ..
Last edited:
