How do I draw the diagram of the mirror charge

[blueyellow]

Homework Statement

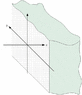
Two point charges +q and -q are placed respectively in positions (-a, 0, +a) and (-a, 0, -a) of a cartesian reference frame, with a being positive and known. The half space of positive x is fully occupied by a conductor. What are the positions and values of the mirror charges in this specific case?

The mirror charge for +q is: -q at (a, 0, +a)
The mirror charge for -q is: +q at (a, 0, -a)

DRAW A SKETCH
how do I do this considering that 'the half-space of positive x is fully occupied by a conductor'

The Attempt at a Solution

drawing a line at y=0, z=0 on the x-axis but only for positive x
but this is wrong

 

[gneill]

What geometrical object describes the interface between the filled half-space and the unfilled half space?

 

[blueyellow]

all i could picture was this semi-infinite block filling the positive x space. but since you said the word 'interface' does it mean i can just sort of not see it as a block, and just see it as an infinite plane on the y-z plane? so i sketch the y-z plane?

 

[SammyS]

Everything is at y = 0, so I suggest you draw/sketch the zx-plane .

 

[cupid.callin]

"The half space of positive x is fully occupied by a conductor"
i can't understand this line?
which space?

 

[gneill]

all i could picture was this semi-infinite block filling the positive x space. but since you said the word 'interface' does it mean i can just sort of not see it as a block, and just see it as an infinite plane on the y-z plane? so i sketch the y-z plane?

You can sketch the yz plane and indicate that to the +x side is conductor, and to the -x side is empty space. If you want to get fancy, you can indicate a portion of the conductor region as a 'cutaway' section, implying that it extends indefinitely. Something like this:

https://www.physicsforums.com/attachment.php?attachmentid=37208&stc=1&d=1310746184