moondaaay
- 2
- 0
1.
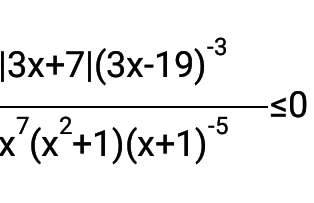
Solving Polynomial Inequalities
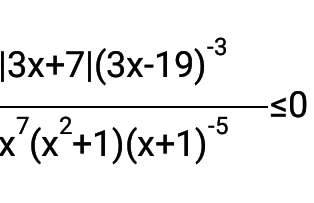
Then I used the property of absolute value inequality to get rid of it.
But I really don't know if I'm doing the right step. Is this correct? So that I could separate them in two cases and find the solution set.
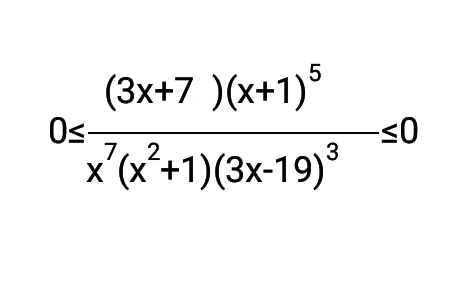
Homework Equations
Solving Polynomial Inequalities
The Attempt at a Solution
Then I used the property of absolute value inequality to get rid of it.
But I really don't know if I'm doing the right step. Is this correct? So that I could separate them in two cases and find the solution set.