Johnny Leong
- 48
- 0
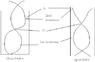
Illustrate the modes of vibration of the fundamental and the first two overtones when a musical note of fundamental frequency 256 Hz (cycles per second) is produced by air in a tube:
(i) open at both ends;
(ii) closed at one end.
Mark nodes and antinodes of displacement N and A respectively.
Ans: Please see my figure. Is my drawing right? Anythign wrong?
State the frequencies of each pair of overtones.
Ans: The frequencies of overtones are 3*256 Hz and 5*256 Hz respectively, right?
Why a musical note produced by an open tube or pipe more mellow than a note of the same fundamental frequency produced by a closed tube?
Ans: Because the antinodes are produced at both ends in an open tube, the sound is weakened.
(i) open at both ends;
(ii) closed at one end.
Mark nodes and antinodes of displacement N and A respectively.
Ans: Please see my figure. Is my drawing right? Anythign wrong?
State the frequencies of each pair of overtones.
Ans: The frequencies of overtones are 3*256 Hz and 5*256 Hz respectively, right?
Why a musical note produced by an open tube or pipe more mellow than a note of the same fundamental frequency produced by a closed tube?
Ans: Because the antinodes are produced at both ends in an open tube, the sound is weakened.
Attachments
Last edited: