How Do You Analyze the Function \( f(x) = \frac{x-4}{x^3} \)?

[kald13]

Homework Statement

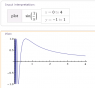
I am to explain all intercepts, critical numbers, extrema, inflection points, and asymptotes of the function f(x)=(x-4)/x^3.

2. The attempt at a solution

a) The y-intercept does not exist, as the domain of the function is all real numbers except x=0. Solving the numerator for 0 yields an x-intercept at x=4
b) f'(x) is easily calculated to be (12-2x)/x^4; solving the numerator for 0 yields a critical number of x=6, and x is undefined at 0, yielding our second critical number; Using values from the intervals shows f'(x)>0 on (-infinity, 0] and [0, 6); f'(x)<0 on (6, infinity), indicating what appears to be a local maximum at x=6. Plugging this into f(x):

f(6)=(6-4)/6^3
f(6)=2/216 or 1/108

I note that this is a positive number, where f(2) is negative, meaning the line has crossed the x-axis between 2 and 6 (specifically at x=4, as predicted)

f(2)=(2-4)/2^3
f(2)=-2/8 or -1/4

Inflection points and second derivative information aside, I now come to the point where I am trying to predict the behavior of the function as x approaches positive and negative infinity.
c) I know there is a vertical asymptote at x=0 due to the fact that the limit of the function does not exist as x approaches 0, but what about horizontal asymptotes?

limit as x approaches infinity of (x-4)/x^3

This is indeterminate, infinity divided by infinity, so using L'Hospital's rule I take the derivative of the numerator and denominator for

limit as x approaches infinity of 1/(3x^2)

I factor out constants:

(1/3) limit as x approaches infinity of 1/x^2

And I know that the limit of 1/x is 0. But here's my problem: I already know that my function has crossed the x-axis at 4, so how can there be a horizontal asymptote at y=0?

 

[scurty]

And I know that the limit of 1/x is 0. But here's my problem: I already know that my function has crossed the x-axis at 4, so how can there be a horizontal asymptote at y=0?

Asymptotic behavior is based on how the distance between the function curve and the asymptote line approaches zero as they branch out to infinity. How the function behaves before then is irrelevant. Take for example the graph of $f(x) = \sin(1/x)$. As x values approach 0 from either side, the function crosses the x-axis an infinite number of times. Yet $\displaystyle\lim_{x \rightarrow \pm\infty} \sin(1/x) = 0$.