How Do You Calculate Average Power in an AC Circuit with Phasors?

[ineedmunchies]

Ok I've been given a problem that I've got stuck on, I was wondering if anyone here could help.

Q:
v(t) = 100 sin(200t+20^)
i(t) = 10 sin(200t-10^)
Express voltage and current as phasors, and calculate the average power being supplied. (I've used ^ to denote degrees)

The phasors part is pretty simple I think, the voltage is a line 100 in magnitude and 20 degrees positive of the x axis, and the current is of 10 magnitude and 10 degrees negative of the x axis.

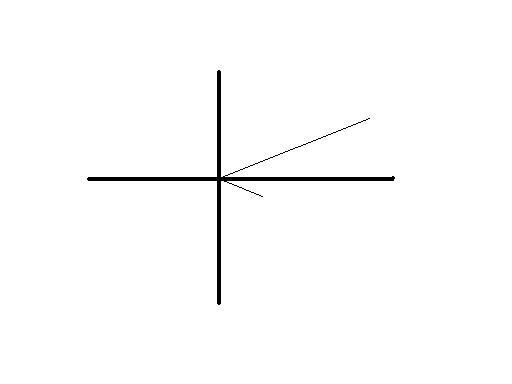
Its the power bit that I don't get, should I break these down into complex form and multiply them that way?

 

[ranger]

The phasors part is pretty simple I think, the voltage is a line 100 in magnitude and 20 degrees positive of the x axis, and the current is of 10 magnitude and 10 degrees negative of the x axis.

Be careful here. v(t) and i(t) are given in peak values. Phasors are represented in RMS or effective values.

To find ave. power, you need to find the power factor. Which is the cos(theta), where theta is the angle difference between the i(t) and v(t).

P_ave = (Vm*Im)/2 * cos(theta)
Where Vm and I am are the peak values of v(t) and i(t), respectively.

 

[ineedmunchies]

Oh I forgot about them being in rms, that means they should be .707 times the peak values, because they are sinusoidal?

And theta would be 30 degrees?

 

[ranger]

Oh I forgot about them being in rms, that means they should be .707 times the peak values, because they are sinusoidal?

Correct.

And theta would be 30 degrees?

Correct also.
Dont forget that cosine of a positive and negative theta gives the same result. So it won't matter which angle you subtracted from what.