How Do You Calculate Displacement from Town B to Town C?

[MercifulBoss]

Having a basic and fundamental knowledge of Physics, I was able to solve the Following question:

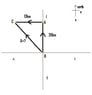
Town A lies 20 km North of town B. Town C lies 13 km West of town A. A small plane flies directly from town B to C. What is the Displacement of the Plane?

a) 33 km [W 33degrees N]
b) 19 km [W 33degrees N]
c) 24 km [W 57degrees N]
d) 31 km [W 57degrees N]
e)6.6 km [W 40degrees N]


My answer was a).

I got my answer by adding 20 and 13. Is this correct?

 

[robertm]

HI mercifulboss, actually the answer is C)24 Km.

Try drawing a simple overview of the situation:

The question is trying to simply test your knowledge of the pathagareom theorem.
the path that the plane travels from B to C is the Hyperbole of a triangle made by A, B, and C. If you simple us the equation: A^2 + B^2 = C^2
you get: C^2 = 579 km.
So then: C = 24 km.

 

[MercifulBoss]

HI mercifulboss, actually the answer is C)24 Km.

Try drawing a simple overview of the situation:

View attachment 13530

The question is trying to simply test your knowledge of the pathagareom theorem.
the path that the plane travels from B to C is the Hyperbole of a triangle made by A, B, and C. If you simple us the equation: A^2 + B^2 = C^2
you get: C^2 = 579 km.
So then: C = 24 km.

Thank you.

But when do you add up 20 and 13? In what situations?

 

[robertm]

Well as far as trigonometry goes you wouldn't really ever need to do that. There isn't a certain formula that requires that operation. However it does depend on the situation and there could be a million different possibilities for needing to add those, just not this one

 

[dumdum000333]

if the question had stated that the plane went from b to a to c and asked for the distance traveled you would answer 33, but since it asked for displacement path traveled does not matter, only the straight distance from c to b

 

[Vishal60]

so we need x

therefore X=20(j) + 13(-i)
______________
lXl=/ (20)^2+(13)^2
_____
=/ 569
= 23.88~24km

 

[malawi_glenn]

Vishal60: Never post full solution!

Read and follow the rules.