How Do You Calculate Normal Force and Tension Direction at Point O?

[laimonel]

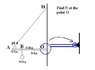
2. Homework Equations : N=mg; M=Fl
3. The Attempt at a Solution : i find that the normal force of the rope AD is 8.5N.

Hello.
Sorry that in my first post I'm already asking for help, but I'm getting really desperate with this problem. I need to find the Normal force at the point O and direction of it. I tried multiplying the N of the rope times cos of 45° but it's not right.
The answer should be: 7.2N, 57° vertical.
Thanks in advance.
P.S. I apologise for my bad english.

 

[JHamm]

Maybe I'm missing something here but a normal force is perpendicular to the surface and the only two surfaces involved at O are at 0 and \frac{\pi}{2} so where 57^o comes from I have no idea.

 

[laimonel]

Maybe I'm missing something here but a normal force is perpendicular to the surface and the only two surfaces involved at O are at 0 and \frac{\pi}{2} so where 57^o comes from I have no idea.

That is exactly what i was thinking, but the book says otherwise..
Well actually it says "find reaction force having in mind that point O car rotate when it's not balanced". And i assume that by "reaction force" it means normal force.

 

[ehild]

Well actually it says "find reaction force having in mind that point O car rotate when it's not balanced". And i assume that by "reaction force" it means normal force.

If the rod can rotate around O then it is connected to a hinge, and the reaction force comes from the pin through the hinge, fixed to the wall. The reaction force of the pin can be of any direction. I drew the hinge into your picture.

ehild

 

[NascentOxygen]

Well actually it says "find reaction force having in mind that point O car rotate when it's not balanced". And i assume that by "reaction force" it means normal[/color] force.

I think you are translating the textbook wrongly. On force diagrams, the word "normal" means perpendicular to a line or surface. The force at 0 will have both a vertical and horizontal component, so the sum of these components means the reaction at O can not be exactly perpendicular to the vertical support.

To solve the problem, you will need to take moments about a couple of convenient points. One of these is point D. So as part of your working, you'll need the vertical height DO.

 

[technician]

You should draw the forces on the diagram.
As well as the reaction force at O which you are trying to find there is a Tension in the string, The weight due to the 0.6kg object at B and the weight of the beam itself (presumably this is uniform)