rico22
- 51
- 0
Homework Statement
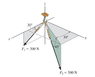
a) Express each force as a Cartesian vector.
b) Determine the magnitude and coordinate direction angles of the resultant force acting on the hook.
See figured attached.
Homework Equations
The Attempt at a Solution
First I expressed F1 and F2 into its x, y, and z components.
F1: 300(cos 30°)\hat{}i +0\hat{}j -300(sin30°)\hat{}k... this gives 260\hat{}i +0\hat{}j -150\hat{}k
F2: 500(cos 45)(sin 45) + 500(cos 45)(cos 30) - 500(sin 45)
250\hat{}i + 306\hat{}j - 354\hat{}k
Resultant (FR) = F1 + F2: 510\hat{}i +306\hat{}j - 504\hat{}k
magnitude of resultant = √(5102+3062+(-504)2) ≈779 N
θx= cos-1(510/779) ≈49°
θy= cos-1(306/779) ≈67°
θz= cos-1(504/779) ≈130°
But this is wrong its supposed to be magnitude of resultant = 733N with angles of 53.5, 65.3, 133 respectively. I don't really know what I am doing wrong. Any type of help would greatly be appreciated.